Electric field due to two positive charges

[sebah]

I am having trouble solving the following problem. I am given two positive charges on the x axis:

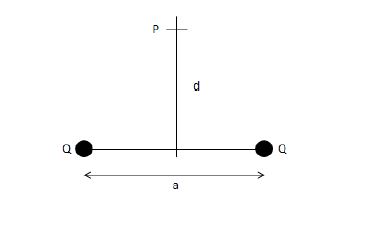
I know that the electric field strength at point P is $E=150 \frac{V}{m}$, $d=1.8m$ and $a=2.5m$. I want to find the charge of $Q$. As far as I know, the electric field on the y-axis between the two charges is given by:

$$E=\frac{2xQ}{4 \pi \epsilon_0 (x^2+y^2)^{\frac{3}{2}}}$$

where $x$ is the distance between one charge and the origin and $y$ is the distance from the origin on the $y$-axis. In this case $y=d$ and $x=\frac{a}{2}$.

$$E=\frac{aQ}{4 \pi \epsilon_0 ((\frac{a}{2})^2+d^2)^{\frac{3}{2}}}$$

Solving for $Q$:

$$Q=\frac{E 4 \pi \epsilon_0 ((\frac{a}{2})^2+d^2)^{\frac{3}{2}}}{a}$$

Plugging in values gives me:

$$Q=7.02 \cdot 10^{-8} C=70nC$$

The correct answer is supposed to be $~50nC=50\cdot 10^{-9}C$. Am I doing something wrong or is there a mistake in the solution?

 

[hutchphd]

Does your value for E make sense in the limit x=0??

 

[sebah]

Does your value for E make sense in the limit x=0??

Not really I think. If x=0 which means that the distance between the charges goes to zero (a=0) I get E=0. Not sure why I am getting zero here though. Should be something like the electric field of 2Q at the origin.

 

[scottdave]

If I were doing it, I would just do the vector sum of field from each charge. What is the net vector at point P?

 

[hutchphd]

Not really I think. If x=0 which means that the distance between the charges goes to zero (a=0) I get E=0. Not sure why I am getting zero here though. Should be something like the electric field of 2Q at the origin.

Where did you get the formula? Its wrong.

 

[sebah]

If I were doing it, I would just do the vector sum of field from each charge. What is the net vector at point P?

That's exactly what I did. My formula looks just like the one derived by R. Shankar in his yale physics course. LINK

 

[sebah]

Where did you get the formula? Its wrong.

Like I mentioned in the other reply I got the formula from R. Shankar and his yale course. LINK

 

[RPinPA]

In the lecture, he is calculating the field of a dipole where one charge is positive and one is negative. The y-components cancel out and the x-components add.

That's not the case here. Draw the vectors representing the fields from those two identical positive charges. They do not cancel out in the same way as the fields in your link.

Moral: Don't take formulas blindly from one situation and apply them to a totally different situation.

 

[sebah]

In the lecture, he is calculating the field of a dipole where one charge is positive and one is negative. The y-components cancel out and the x-components add.

That's not the case here. Draw the vectors representing the fields from those two identical positive charges. They do not cancel out in the same way as the fields in your link.

Moral: Don't take formulas blindly from one situation and apply them to a totally different situation.

Oh I see. In my case the horizontal components cancel and the vertical components add. I will then get:

$$E=\frac{2*y*Q}{4 \pi \epsilon_0 (x^2+y^2)^{\frac{3}{2}}}$$

 

[vanhees71]

Hint: an electric field is a vector!

 

[hutchphd]

Incidentally, you should be able to write down the electric field from point charges from first principles. In fact the easy way to do this is to notice the symmetry, write down the electric (scalar) potential and take the derivative d/dy to get the field in that direction. But any correct way is OK.