Electric field lines from very long cylinders and thin disks

[schrodingerscat11]

Homework Statement

Good day everyone. I am studying Gaussian cylindrical surfaces. I have three questions:

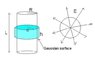
(1) Books would say that the electric field lines would emanate from the lateral side of the cylinder and that the ends will not contribute anything. I cannot understand this because if I have a charged cylinder, I picture field lines to be emanating and perpendicular from the entire cylinder surface including the top and end part. Can you explain why are the ends not contributing to the flux ψ=∫E da? Wouldn't electric field lines parallel to da on top and end of cylinder (if there is such a thing) contribute to the total flux?

(2) I picture a thin disk (example is a coin) as a cylinder with a very small height. But when we get the electric field of such, we just assume that electric field emanates from the "face" of the disk and not from the sides. Why wouldn't field lines emanate also from the sides as it would does for ordinary cylinders? Wouldn't electric field lines leave charged solid volumes in the same way for same shape? Why would electric field lines emanate differently for cylinders of varying thickness and height?

(3) Also, if you have a very large plane of charge. I was wondering why electric field lines wouldn't emanate from the fringes of the plane and parallel to the plane. I was thinking of the plane as a collection of smaller charges dq and that the electric field from each adjacent dq would cancel. But at the sides, there is none to cancel the E-field due to outermost dq so field lines from the edges should also contribute and point parallel to the plane.

Homework Equations

$\int E \cdot da = \frac {q_{enc}}{ε_o}$

$E = \int \frac {dq ~\hat{r}}{r^2}$ where r is the vector from the source to the location of electric field.

The Attempt at a Solution

I think most of my thoughts are expressed in the question part. Thank you very much. :shy:

 

[ChiralWaltz]

1) calculate the flux of one face and then calculate the flux of the other. Remember that equation reads E (dot) dA or (E)(A)cos(theta) once integrated. The cosine is taken with respect to the e-field and is normal to the face's surface.

The symbol for flux is phi, not psi.

2) E-fields experience what is known as fringing effects around the edges of the disks. In the second semester physics course they are not addressed mathematically.

3) I'm not sure.

We learning introductory information, many authors go for giving a general understanding of the phenomena. An example would be ignoring air friction when calculating the time it takes for an apple to fall in the first semester of physics. This is done so we may focus on the concept at hand and not get lost on the finer points that are explored later.

 

[schrodingerscat11]

Hi! Thank you very much for the reply and sorry for the very late response, I had a very busy week last week.. :(
Anyway,..
1) The answer would be what is given in the book if I assume that E-fields are all emerging from the lateral side of the cylinder. But again, I think of E-fields as coming from all sides like B-fields emerge from a magnet. The only difference is that E-field are all directed outward from the body. So at top face, there are emerging E-fields perpendicular to the face (i.e. parallel to the normal vector of the cylinder face).
2) I've heard of this before. But I forgot.. I'll look for it in my notes. And in connection with your last paragraph, I know that in science there are a lot of factors left out. But even so, the equations should beequivalent. (E.g. Newton's Equations are equivalent with Einstein's equations, if we let v<<c) I guess what I really wanted was a general equation for E-field of cylinder such that if I let the height of cylinder approach infinity, I'll get the E-field equation for an infinite line of charge and if I let r approach zero, I'll get the Electric field of a thin disk.

But thanks anyway. :)

 

[ChiralWaltz]

I do not have Internet at my place so I will have to edit this to make sure your questions are being answered in full.

Here is an earlier discussion on fringing:

https://www.physicsforums.com/showthread.php?t=124150

1) I'm thinking about the e-field

 

[electronicsguy]

1. If it was mentioned in the book that height of cylinder >> diameter of cylinder, (much like a wire), then the top and bottom surface of the cylinder would be negligible.
2. Same as number one but in here, the diameter >> height of cylinder.
3. Electric Field would still emanate from the fringe of the plane. If a point charge is placed parallel to the fringe of the plane, then the charge will experience an electric field from the plane where the plane acts as a line charge. (Most problems dealing with plane charge does not have its point parallel to the fringe of the plane)

Also if you use psi then ψ=∫DdA and if you used phi then Φ=∫EdA, (Note: ψ = Charge enclosed and
Φ = Charge enclosed/Permittivity) where D = Electric Flux Density. D= εE)

 

[schrodingerscat11]

I do not have Internet at my place so I will have to edit this to make sure your questions are being answered in full.

Here is an earlier discussion on fringing:

https://www.physicsforums.com/showthread.php?t=124150

1) I'm thinking about the e-field

Thanks! I do not understand everything as I skimmed this.. But this would help.. Thanks again...

 

[schrodingerscat11]

1. If it was mentioned in the book that height of cylinder >> diameter of cylinder, (much like a wire), then the top and bottom surface of the cylinder would be negligible.
2. Same as number one but in here, the diameter >> height of cylinder.
3. Electric Field would still emanate from the fringe of the plane. If a point charge is placed parallel to the fringe of the plane, then the charge will experience an electric field from the plane where the plane acts as a line charge. (Most problems dealing with plane charge does not have its point parallel to the fringe of the plane)

Also if you use psi then ψ=∫DdA and if you used phi then Φ=∫EdA, (Note: ψ = Charge enclosed and
Φ = Charge enclosed/Permittivity) where D = Electric Flux Density. D= εE)

@electronicsguy
(1) Yeah, it was mentioned as a "very long cylinder." The topic is Gauss's Law by the way. What I didn't like was that the discussion just said that the ends contribute nothing to the flux (so that means totally zero) when what it really means was that the flux from ends are negligible. That's two different things.
(2) Yeah, that too.
(3) That's what I thought. If there is a point charge at the fringe, shouldn't it move? But again, if we use Gauss's Law, we'll end up with the electric field of the infinite plane of charge being E=$\frac{σ}{2ε}$ that emerges from the faces of the planes. None from the edges!

So I thought if that is the case, a point charge near the edge of plane should not move. But this doesn't make sense to me because it should move. So maybe Gauss's Law might be leaving out something. Thanks for confirming my thoughts.

(About the ψ symbol, I didn't know that.. Haha... I was in a hurry and I can't find the phi symbol from quick symbols so I just used ψ. Sorry about that. I didn't know it has another meaning.)

 

[electronicsguy]

I think you misunderstood (3). E=σ/2ε means the Electric Field intensity at a point due to an INFINITE plane charge where σ = Surface Charge Density. It was derived by integration using dE = (dQ/4∏εR^2)aR where aR is the unit vector from charge to point and having R as the distance and using σ = dQ/dA and dA = dxdy (Using rectangular coordinates system. Its better to use cylindrical coordinates dA = ρdρdø), the resulting equation will be E=σ/2ε. Since the plane is infinite, the point cannot be located parallel to the fringe because that means the point is within the plane itself because infinite plane has no ends. E=σ/2ε tells us that the electric field intensity due to an INFINITE plane charge does not depend on the distance from the test point to the plane charge.

So if we want to find E at a point facing the plane due to a plane charge, the Electric Field emanating from the face of the plane will be the one contributing E and the E emanating from the edge will not contribute E since the flux lines (from the fringe) will not intersect the point.

A point charge placed parallel to the edge of a plane charge (which is not infinite ) will definitely move.
If you have doubts, you can always work on the math starting from dE = (dQ/4∏εR^2)aR

 

[ehild]

I am studying Gaussian cylindrical surfaces. I have three questions:

(1) Books would say that the electric field lines would emanate from the lateral side of the cylinder and that the ends will not contribute anything.

The Gaussian surface is not the same as the surface of the total cylinder (or disk or plate). One usual problem says that the charge is distributed evenly on the surface of an empty cylinder of length L and radius R<<L, and the surface charge density σ is given; what is the electric field at a point opposite to the middle of the cylinder at distance d<<L from its axis.
You take a Gaussian surface in form of a short concentric cylinder (high h<<L) at the middle of the cylinder (far from the ends) The electric field is radial there by symmetry, so there are no field lines crossing the top and bottom plates of the Gaussian cylinder. The net flux through the Gaussian is (2πdh)E, the enclosed charge is q=2πRhσ, so E(d)= (σ/ε₀)(R/d).
The problem can also say that it is an insulating cylinder of net charge Q, distributed evenly in the volume. In this case, the enclosed charge in the Gaussian is Q V(Gaussian)/V(cylinder).

If the cylinder is from metal and the net charge is given, then the charge is not distributed evenly, but the potential is constant on the surface. If you are a teacher, you have to choose the geometry of the cylinder so as that charge near the edge is negligible to the total charge of the cylinder, otherwise a smart student asks you inconvenient questions. You had better avoid problems like that.

You, as a student, have to read the problem text very carefully before starting to solve it.


ehild

 

[schrodingerscat11]

I think you misunderstood (3). E=σ/2ε means the Electric Field intensity at a point due to an INFINITE plane charge where σ = Surface Charge Density.

Oh right. I think I confused E=σ/2ε as valid for finite plane of charge. I see my mistake now. Thank you electronicsguy.

 

[schrodingerscat11]

The Gaussian surface is not the same as the surface of the total cylinder (or disk or plate). One usual problem says that the charge is distributed evenly on the surface of an empty cylinder of length L and radius R<<L, and the surface charge density σ is given; what is the electric field at a point opposite to the middle of the cylinder at distance d<<L from its axis.
You take a Gaussian surface in form of a short concentric cylinder (high h<<L) at the middle of the cylinder (far from the ends) The electric field is radial there by symmetry, so there are no field lines crossing the top and bottom plates of the Gaussian cylinder.

Ah, I see, because the Gaussian surface is inside the actual surface, even the top and bottom plates would have E-fields emerging radially from the axis. Hence, the Gaussian surface would only have E-field emerging from lateral sides. Thank you very much ehild. :)

 

[electronicsguy]

Oh right. I think I confused E=σ/2ε as valid for finite plane of charge. I see my mistake now. Thank you electronicsguy.

Glad to help :)