Electric Field Shielding: Does a Conductor Shield Inside?

[arestes]

Hi.
I was reading about conductors in electrostatic equilibrium and how it makes sense that they have zero electric field inside the material even when an external charge is brought near. The charge density of the material just rearranges itself to cancel. Then I searched for hollow conductors since they behave differently.

However, the derivations of the fact that there is zero field inside a conductor (both hollow and solid) uses symmetry.
Using Gauss' law and this symmetry, when there's no charge outside, it can easily be seen that the magnitude of the field is the same at a specified distance of the center and it clearly means that a gaussian surface enclosing no charge implies a zero field.
I am worried of this last step because when an external charge is brought near, there is no spherical symmetry anymore. ¿Is the field inside shielded completely? Or, ¿is this just an approximation of a "Faraday Cage"? (does it work the same when the sphere is hollow and when it's solid?).

I found a Wiley resource that says it's not zero:

But I also found another resource (both on google) that asks the same but, the answer it gives is zero:
https://www.liveworksheets.com/oi1233136al

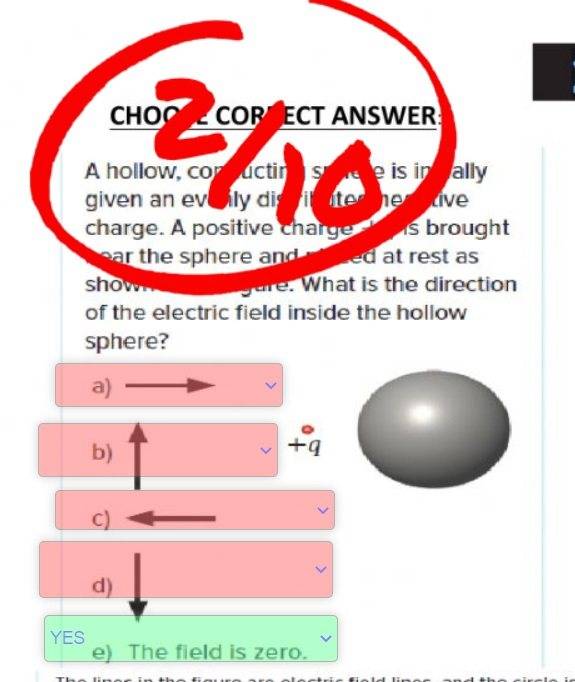
(By the way, this other question is in many websites but I'm not sure what book this has been taken from, does anyone know?).

So... does a (hollow or solid) spherical conductor with an external point charge completely shield off electric fields inside it?
Also, I have a feeling it doesn't. I read wikipedia's article about image charges with this method of "mirror images" and it's supposed to act as if there was another charge inside of opposite sign. Does this work with solid or hollow. I couldn't find.

ThanksI

 

[BvU]

However, the derivations of the fact that there is zero field inside a conductor (both hollow and solid) uses symmetry.

No it does not. It uses Gauss's theorem.

 

[arestes]

No it does not. It uses Gauss's theorem.

Yes, that's what I say, but Gauss' law alone is not enough if we can't factor out the electric field outside the integral due to symmetry, right?

 

[kuruman]

Unless there are charges inside the hollow conductor, the electric field inside the cavity is zero. Whoever put a box around (c) in Wiley's resource goofed.

 

[kuruman]

Yes, that's what I say, but Gauss' law alone is not enough if we can't factor out the electric field outside the integral due to symmetry, right?

Gauss's law guarantees that there is no charge inside a Gaussian surface that is drawn just under the surface of the conductor. You need to add that if there were an electric field inside the cavity, then one should be able to draw an electric field line from one point A of the cavity to another point B. However that means that there is a potential difference V_AB from one point of the conductor to another which violates the fact that conductors in static conditions are equipotentials. This argument is also known as invoking the Uniqueness Theorem in electrostatics.