Electric Flux for a cube problem

[vcsharp2003]

Homework Statement

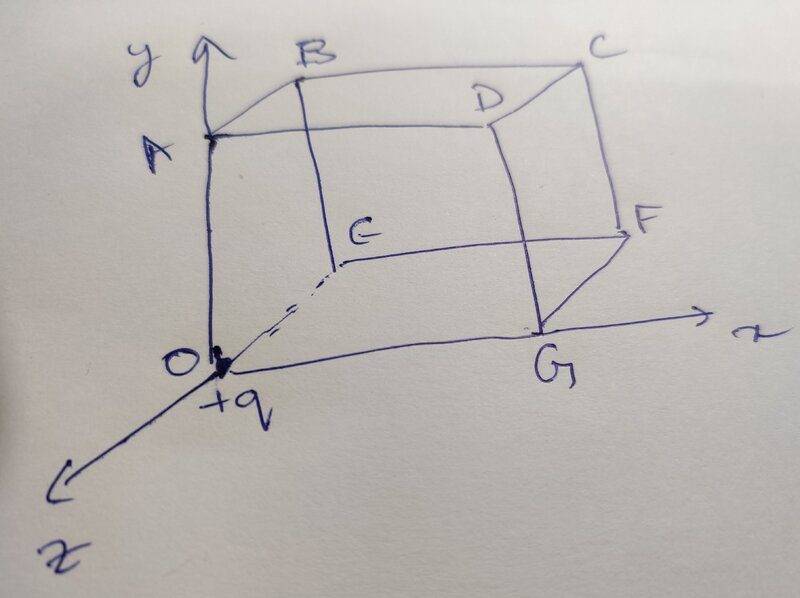
An electric charge q is placed at one corner of a cube of side L. What is the flux through each face of the cube?

Relevant Equations

$\phi = \frac {q} {\epsilon_0}$, which is the Gauss's Law in electrostatics

I have tried to understand the solution given in the book which is as pasted below. The solution uses Gauss's Law but makes no mention of which Gaussian surface is used. The diagram that I have used to understand this problem is also given at the end. From the diagram, faces OADG, OABE and OEFG have zero flux since lines of force skim through these faces. The other three faces BCFE, CDGF and ABCD have lines of force cutting them and therefore will have non-zero flux.

 

[robphy]

The Gaussian surface to choose is the surface you are interested in.
So, to find the flux through the faces of the cube, choose as your Gaussian surface: the faces of the cube [a closed surface].

 

[vcsharp2003]

The Gaussian surface to choose is the surface you are interested in.
So, to find the flux through the faces of the cube, choose as your Gaussian surface: the faces of the cube [a closed surface].

Sorry, I didn't get you. Did you mean to select the cube as the Gaussian surface? If we select the cube as a Gaussian surface then it has no charge inside it and therefore flux would be 0 passing through this closed cube surface according to Gauss's law.

 

[robphy]

Consider the cube with a corner at the origin and edge length s.
Also consider the larger cube with edge length 2s, with center at the origin.

 

[vcsharp2003]

Consider the cube with a corner at the origin and edge length s.
Also consider the larger cube with edge length 2s, with center at the origin.

So, it's like saying there is a cube of side s in each octant of the xyz axes system, such that they all have one corner at origin O. Is that correct?

 

[Delta2]

Also consider the larger cube with edge length 2s, with center at the origin.

That's the gaussian surface the book chooses. And the 3 outer faces of the smaller cube with edge s are 1/8 of the aforementioned gaussian surface.

 

[vcsharp2003]

That's the gaussian surface the book chooses. And the 3 outer faces of the smaller cube with edge s are 1/8 of the aforementioned gaussian surface.

The Gaussian surface would look something like below and the cube of interest would be in the octant defined by postive x, postive y , negative z octant.

 

[vcsharp2003]

That's the gaussian surface the book chooses. And the 3 outer faces of the smaller cube with edge s are 1/8 of the aforementioned gaussian surface.

Considering such a Gaussian surface, we could then say that the total flux emanating out of the gaussian surface is $\phi = \frac {q} {\epsilon_0}$. Since there are six faces of the large cube that are symmetrically placed about the charge at origin, so flux would be same for each large face and it would be $\phi_{lf} = \dfrac {1} {6} \frac {q} {\epsilon_0}$. Now, each face of larger cube will have 4 faces of smaller cube (of side s) as shown in diagram. Therefore, flux through each small face $\phi_{sf} = \dfrac {1} {4} \dfrac {1} {6} \frac {q} {\epsilon_0}= \frac {q} {24\epsilon_0}$.

 

[Delta2]

Considering such a Gaussian surface, we could then say that the total flux emanating out of the gaussian surface is $\phi = \frac {q} {\epsilon_0}$. Since there are six faces of the large cube that are symmetrically placed about the charge at origin, so flux would be same for each large face and it would be $\phi_{lf} = \dfrac {1} {6} \frac {q} {\epsilon_0}$. Now, each face of larger cube will have 4 faces of smaller cube (of side s) as shown in diagram. Therefore, flux through each small face $\phi_{sf} = \dfrac {1} {4} \dfrac {1} {6} \frac {q} {\epsilon_0}= \frac {q} {24\epsilon_0}$.

View attachment 289482

Yes I think the above logic is correct too and it gives the same result as book.