Why are my force equations giving me incorrect answers?

[cwill53]

Homework Statement

An electric lamp weighing 5lbs is suspended by a cord AB from the ceiling and pulled towards the wall by the cord BC. Determine the tensions $T_{A}$ in the cord AB and $T_{C}$ in the cord BC if the angles $\alpha$ and $\beta$ are $60^{\circ}$ and $135^{\circ}$, respectively. Neglect the weight of the cords.

Ans. $T_{A}$= 3.65 lbs $T_{C}$==2.6 lbs

Relevant Equations

$$\sum \vec{F}=m\vec{a}$$

I had made equations for the forces in the x-direction and y-direction, but when solving them they yielded the wrong answers, which makes me think that they were incorrect:$(T_{A}cos60^{\circ}+T_{C}cos45^{\circ})=0$
$(T_{A}sin60^{\circ}+T_{C}sin45^{\circ})=5lbs$

Here's the diagram for the problem:

 

[BvU]

but when solving them

Can't see where you go wrong if you don't post your work.

Question: in $$T_{A}\cos60^{\circ}+T_{C}\cos45^{\circ}= 0$$ I see four things that are positive. How can that give 0 ?

 

[etotheipi]

$(T_{A}cos60^{\circ}+T_{C}cos45^{\circ})\hat{x}=0$
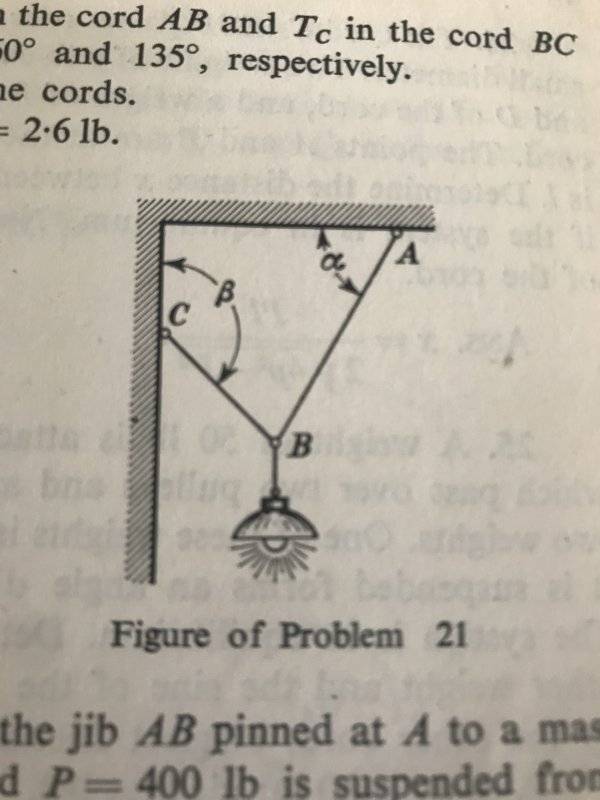
$(T_{A}sin60^{\circ}+T_{C}sin45^{\circ})\hat{y}=5lbs$

Best not to write that; you've got vectors on the LHS and scalars on the RHS. Also, as @BvU pointed out, the first equation should be setting off alarm bells!

Look at your first equation. You know that $\sum F_x = ma_x = 0$ here. What is the $x$ component of the force exerted by the member BC?

 

[cwill53]

Can't see where you go wrong if you don't post your work.

Question: in $$T_{A}\cos60^{\circ}+T_{C}\cos45^{\circ}= 0$$ I see four things that are positive. How can that give 0 ?

I don't see any other forces in the x-direction.

 

[cwill53]

Should it be $(T_{A}cos60^{\circ}-T_{C}cos45^{\circ})=0$?

 

[BvU]

If I pull to the left and you pull to the right, and we pull with equal forces, will something in the middle accelerate twice as fast as when I pull alone ? Or will it stay in place ?

Nice drawing, but physics sketches should be restricted to the bare essentials

 

[BvU]

Should it be $(T_{A}cos60^{\circ}-T_{C}cos45^{\circ})=0$?

Yees. Why ?

 

[cwill53]

Yees. Why ?

Because that's the only way that makes sense if the system isn't accelerating. You can't add two positive numbers and get 0.

 

[etotheipi]

Should it be $(T_{A}cos60^{\circ}-T_{C}cos45^{\circ})\hat{x}=0$?

Pretty much, but it should be either

$(T_{A}cos60^{\circ}-T_{C}cos45^{\circ})\hat{x}=\vec{0}$

or

$T_{A}cos60^{\circ}-T_{C}cos45^{\circ} = 0$.

As for the trouble with signs, $\vec{T}_C = \vec{T}_{Cx} + \vec{T}_{Cy} = T_{Cx} \hat{x} + T_{Cy} \hat{y}$. If you draw the component vectors in the $x$ and $y$ directions, you know that $\vec{T}_{Cx} = T_{Cx} \hat{x}$ has to point to the left (i.e. in the $-\hat{x}$ direction). This should give you some clues as to the required sign of $T_{Cx}$...

 

[cwill53]

If I pull to the left and you pull to the right, and we pull with equal forces, will something in the middle accelerate twice as fast as when I pull alone ? Or will it stay in place ?

Nice drawing, but physics sketches should be restricted to the bare essentials

It will stay in place because the forces will cancel out.

I like to draw the pictures for reference in the future; this book is long out of print.

 

[etotheipi]

I like to draw the pictures for reference in the future; this book is long out of print.

I mean it seems you've got the knack for it... just make sure not to spend too long on the shading...

It might also help to draw the unit vectors you're using on the diagram as well. Just so that when you see the force is acting in the negative $x$ direction, you can go 'aha', the coefficient of $\hat{x}$ has to be negative so $F_x < 0$.

 

[cwill53]

I mean it seems you've got the knack for it... just make sure not to spend too long on the shading...

It might also help to draw the unit vectors you're using on the diagram as well. Just so that when you see the force is acting in the negative $x$ direction, you can go 'aha', the coefficient of $\hat{x}$ has to be negative so $F_x < 0$.

Thanks, I'll do that from now on.

@BvU @etotheipi Thanks for the help, that fix did the trick.