Electric potential at the bottom of a ring?

[lz975545]

Homework Statement

[/B]
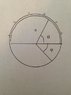
A circular ring of radius "a" has a total charge Q uniformly distributed along the top half. (Q is distributed along the semicircle in quadrants I and II). What is the potential at a point located on the bottom of the ring (observation point is on the ring in quadrant III or IV). The location of the observation point is described as being located at an angle φ measured from the positive x axis. Find V(a,φ).

Homework Equations

[/B]
V = k ∫ dq / r
λ = dq/dL

The Attempt at a Solution

[/B]
So I substituted λdL for dq to get V = kλ ∫ dL / r but I'm not sure how to get r in terms of a and φ. I'm also not sure how just a semicircle of charge factors into this problem.

 

[gneill]

Hi lz975545,

Welcome to Physics Forums!

You'll want to express dq in terms of dθ so that you can integrate over θ. For the distance between dq and the point of interest on the bottom half of the ring, think in terms of the distance between the points at the ends of the two radius vectors. So there'll be some trigonometry involved.