Electric Potential Distribution in a Vacuum Diode

[HotFurnace]

Homework Statement

This problem is belonging to a book, which is material for Vietnamese students who will take part in IPhO (International Physics Olympiad). Since this problem is written in Vietnamese, I will try my best to translate it to English:
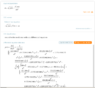
A vacuum diode consists of two parallel conductive plate, each of them has a area of S and their separation is L. The distance between the plates L is very small in comparison to the plates area S. A voltage U is applied to a plate, another plate was grounded. Because of thermal emission of electrons, electrons emitted from cathode will move to the anode (due to the applied voltage U, and the electric field created by another moving electron inside the vacuum space). The thermal emission effect is too great, so that limiting the current flowing thru the diode is impossible (read comment). In this situation we can consider that the electric field at the cathode equals to zero and the electrons velocity at the cathode is also zero. Prove that, the electric potential distribution inside the diode is given by the following equation:
V(x)=U*(x/L)^(4/3)
Find the relationship between U and I (the current flows thru the diode). Do the diode satisfy Ohm's Laws?
The comment (not included in the problem): In my opinion, this means that the diode works in the U/I region before saturation, when the current stays constant even that the applied voltage was increased.

Homework Equations

V(x)=U*(x/L)^(4/3)

The Attempt at a Solution

I tried finding the electron distribution inside the diode, then with superposition principle, I add up the electric field created by the charges distribution and the applied voltage U, then integrate to find the electric potential, but without success. I used Gauss's law differential equation, second Newton laws of motion for a single electron and the hint that current everywhere inside the diode is constant. I manage to find a second order differential equation of V, but it didn't give the answer when solving it.

 

[TSny]

The Attempt at a Solution

I tried finding the electron distribution inside the diode, then with superposition principle, I add up the electric field created by the charges distribution and the applied voltage U, then integrate to find the electric potential, but without success. I used Gauss's law differential equation, second Newton laws of motion for a single electron and the hint that current everywhere inside the diode is constant. I manage to find a second order differential equation of V, but it didn't give the answer when solving it.

Your description of what you tried is not specific enough to evaluate. It would be very helpful if you would show your work in detail.

 

[HotFurnace]

Here's what I had done:
- Apply Gauss's laws for a tiny box region, with surface S, thickness dx, we end up with this equation: $$ρ=ε*\frac {dEe} {dx} (1)$$ in which ρ is the charge density, Ee is the electric field created by the charge (the field created by the voltage U is Ep, the total field is E).
- The current flowing inside this diode must be a constant everywhere inside the diode, regardless of position x. According to the definition of current: $$I=\frac {dq} {dt}=ρSv$$ in which v is the velocity of the electron at position x. Take the differentiation of I we get: $$0=v\frac {dρ} {dx}+ρ\frac {dv} {dx}$$
- The Second Newton laws of motion for one electron is $$e*E=m\frac {dv} {dt}=mv\frac {dv} {dx}$$
- Use substitution, we get the following equation: $$\frac {dρ} {ρ^3}=\frac {eS^2} {mI^2}Edx$$, integrate it, and we get $$-\frac {1} {ρ^2}=\frac {2eS^2} {mI^2}V+C$$ and now I'm unsure what to do, maybe we shall set C=0 and use equation (1) then we will end up with $$ω\sqrt \frac {U} {V} =ε\frac {\partial^2 V} {\partial x^2} $$ ω is the electron density at the anode. Solve this don't works as the solution is very complex.

 

[TSny]

integrate it, and we get $$-\frac {1} {ρ^2}=\frac {2eS^2} {mI^2}V+C$$

I think you are essentially OK up to here, except I don't believe you should have a negative sign on the left. The signs are a headache due to the fact that the electron has a negative charge, the E-field points in the negative x direction, the potential difference equals the negative of the integral of E, etc.

and now I'm unsure what to do, maybe we shall set C=0 and use equation (1) then we will end up with $$ω\sqrt \frac {U} {V} =ε\frac {\partial^2 V} {\partial x^2} $$ ω is the electron density at the anode. Solve this don't works as the solution is very complex.

Yes, you can take the constant C to be zero. It is assumed that the speed $v$ of the electrons can be taken to be essentially zero at the cathode. So the charge density $\rho$ must be very large at the cathode because the current $\rho vS$ has a finite value that is independent of $x$. So, $\frac{1}{\rho^2}$ can be taken to be negligible at the cathode.

The equation $ω\sqrt \frac {U} {V} =ε\frac {d^2 V} {d x^2}$ can be solved easily by first multiplying both sides by $\frac {dV}{dx}$ and then integrating.

Another way to derive the differential equation for $V$ is to set up conservation of energy as $\frac{1}{2}mv^2 = eV$ and solve for $v$. Sub this into $\rho = -\frac{I}{vS}$ where $I$ is the magnitude of the current (so that $I$ is a positive number). Then use this in your equation (1) to get the desired second-order differential equation for $V$. This way, you avoid having to set up and solve a differential equation for $\rho$.

 

[HotFurnace]

Yes! I got the correct answer now. Last time I used Wolfram Alpha to solve the differential equation and then it showed something like this:

It really confused me and led me to the conclusion that the equation was wrong.

 

[TSny]

OK, glad it worked out. Wow, that output from Wolfram Alpha is intimidating! Yikes.