Homework Help Overview
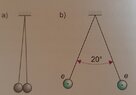
The discussion revolves around the forces acting on two balls hanging from a ceiling at an angle, specifically focusing on the relationship between electric force, tension, and gravitational force. Participants are exploring the balance of forces in both horizontal and vertical directions, as well as the implications of the angle formed by the strings.
Discussion Character
Approaches and Questions Raised
- Participants are attempting to derive equations for the forces acting on the balls, questioning the correctness of initial expressions and exploring the relationships between tension, electric force, and gravitational force. There is also discussion on how to incorporate the angle of the strings into their equations.
Discussion Status
The discussion is active, with participants providing guidance on how to set up equations and questioning assumptions made in earlier posts. There is an ongoing exploration of the relationships between different forces and the geometry of the setup, with no clear consensus reached yet.
Contextual Notes
Some participants note the need to use symbols instead of numerical values in their equations and emphasize the importance of correctly applying trigonometric relationships to the problem. There are also mentions of potential errors in previous attempts, particularly regarding the use of angles in calculations.