Electricity circuit question, amplitude resistor?

[Michael 37]

Homework Statement

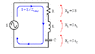
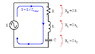
The ac circuit has 3 components in series: a Capacitor C=120μF, an Inductor L=100mH, and a resistor R=7Ω.

A) Find the amplitude of the voltage across the resistor R in the LCR circuit below, when
operated at a frequency of 45 Hz?

B) What is the phase difference between this voltage and
the supply voltage, Vac (= (15 V)cosωt)?

C) At what frequency is this phase difference zero?

D)What is the Q value of this resonant circuit?

Homework Equations

V(t)=Vocos(ωt + ∅)

Z=Vo/Io=R (Z=impedance)

ω=2πf

Q=(ωo)(L)/R

There the only relatable I can find

The Attempt at a Solution

Attempt for part (A) Using V(t)=Vocos(ωt + ∅) I tried searching for Vo as that is the amplitude but we are not given any Voltage? Then I tried using Z=Vo/Io and I found the impedance but then I realized I don't have Io (current). So I was stuck plugging in numbers and trying to manipulate formulae to no avail.

Attempt for part (B) Well I think the voltage amplitude here is 15V with no phase change as ∅ is not present. So I said there is no difference as they must be in phase if there doesn't exist a ∅. Not sure if that is right.

Attempt for part (C) I used Q=(ωo)(L)/R, then I used the fact that ω=2πf which yielded an equation of the form Q=(2π)(f)(L)/R . I plugged in the figures and got a value of 4.04.


Please help! I am very stuck.

 

[gneill]

Hi Michael.

You've used the term "impedance". Have you learned about complex impedance yet, or just reactance, for reactive components (L, C)?

 

[Michael 37]

Hi gneil,

Yes I know how to calculate complex impedance. I think I am pretty comfortable doing so. Is that needed for this particular question? I was thinking that Z should be the complex impedance but that still leaves me with two unknowns whatever equation I use? I wouldn't be too familiar with the reactance components if I am honest.

 

[gneill]

Okay, you're given the frequency of operation. Can you calculate the individual impedances of the capacitor and inductor?

 

[Michael 37]

Yes, the complex impedance of a capacitor is (1/(iwC)) and the Complex impedance of an Inductor is iwL. So I could calculate the individula complex impedances of both comfortably.

 

[gneill]

Yes, the complex impedance of a capacitor is (1/(iwC)) and the Complex impedance of an Inductor is iwL. So I could calculate the individula complex impedances of both comfortably.

So then, what's the total impedance of the series circuit (numerically)?

 

[Michael 37]

This is frustrating. When I use the complex impedance formula for a capacitor to be (1)/(iwC) I get a total circuit complex impedance to be = ((0.042)/(i0.0339)) + 7. The when I use the other capacitor formula for complex impedance -(i)/(wC) I get the total complex impedance of the circuit to = -i0.042 + 7. So lost with the whole question :(

 

[gneill]

Let's do it one step at a time. What are the individual impedances for the components?

 

[Michael 37]

1) Complex Impedance (C.I) of capacitor = 1/(i)(w)(C) where w=2pif.

Therefore plugging it ---> 1/(i)(2pi)(45)(120E-6) = 1/i(29.5)

2) C.I of Inductor = iwL therefore plugging in yields ---> i(2pi)(f)L = (i)(2pi)(45)(100E-3) = i9pi

3) C.I of resistor = R therefore = 7They are all the complex impedances arn't they? What now? Thank you!

 

[gneill]

1) Complex Impedance (C.I) of capacitor = 1/(i)(w)(C) where w=2pif.

Therefore plugging it ---> 1/(i)(2pi)(45)(120E-6) = 1/i(29.5)

Presumably that's meant to be (1/i)(29.5) Ω. Which is -29.5i Ω, after multiplying top and bottom by i. That's a good value. A better one would keep a couple more decimal places as guard digits for future calculations -- Don't round intermediate values.

2) C.I of Inductor = iwL therefore plugging in yields ---> i(2pi)(f)L = (i)(2pi)(45)(100E-3) = i9pi

Something went awry there. $2 \cdot \pi \cdot 45$ is about 283, and multiplying by 100 E-3 can't change the digits...

3) C.I of resistor = R therefore = 7

Correct.

They are all the complex impedances arn't they? What now? Thank you!

Once you've sorted out the inductive impedance value you can write the total impedance for the circuit. Z = ?.

With that you can use Ohm's law to find the current, potential across R, and so on.

And while we're at it, in your first post you calculated the Q using the driving frequency of the source (45 Hz). It should be ω_o as you wrote in the expression for Q. ω_o is the resonant frequency of the RLC circuit.

 

[Michael 37]

Hi.
I fixed the impedances and found the total complex impedance to hold a value of:

-29.5i + 28.3 + 7 = 35.3 - 29.5i = Z total.

but if I were to use ohms law to find the voltage amplitude like part A wants me too would the following be correct: Ohms Law: Zr = Vo/Io = R. Therfore Io = Z/R = 7/7 = 1. Then rearranging Vo = RIo = (7)(1) = 7.

Is that the Voltage amplitude across the resistor? Surely not. And I don't quite understand what you are saying about the Q expression. Thanks

 

[gneill]

Hi.
I fixed the impedances and found the total complex impedance to hold a value of:

-29.5i + 28.3 + 7 = 35.3 - 29.5i = Z total.

Careful, the impedance of the inductor is also imaginary, like the capacitor's. jωL.

but if I were to use ohms law to find the voltage amplitude like part A wants me too would the following be correct: Ohms Law: Zr = Vo/Io = R. Therfore Io = Z/R = 7/7 = 1. Then rearranging Vo = RIo = (7)(1) = 7.

Ohm's law: E = I*Z, so that I = E/Z.

Find the total current I first. Then for individual components with impedance z, E_z = I*z.

Is that the Voltage amplitude across the resistor? Surely not. And I don't quite understand what you are saying about the Q expression. Thanks

The Q of a circuit is related to the resonant frequency ω_o of the circuit by the given formula. The resonant frequency is inherent to the circuit, not determined by the source driving it. You need to find the resonant frequency of the circuit.

 

[Michael 37]

Oh yes my mistake. Ztotal = -1.2i + 7.

Maybe this is me just being an idiot but E is Electric potential or voltage, which we do not have. This is where I keep getting lost. I am obviously wrong but to get the flowing current, we need to know the voltage. We don't have that info yet. All we have is the complex impedance of each component and the frequency...

 

[gneill]

Oh yes my mistake. Ztotal = -1.2i + 7.

Much better. You should get into the habit of keeping a few more decimal places in values that will be used in additional computations. These "guard digits" will prevent rounding errors from creeping into your results.

Maybe this is me just being an idiot but E is Electric potential or voltage, which we do not have. This is where I keep getting lost. I am obviously wrong but to get the flowing current, we need to know the voltage. We don't have that info yet. All we have is the complex impedance of each component and the frequency...

E is the potential (or voltage). I use E rather than V since V is also the unit (Volt). Avoids confusion that way. Since you're not given a specific value for E at this point in the problem, express the result in terms of E.

 

[Michael 37]

Done! :)

Total current I = E/Ztotal = E/(-1.2i + 7) then multiplying by it's conjugate yields:
I total = ( (E)(7 + 1.2i) ) / 50.44

I for the individual componants: For capacitor I = -29.5iE
I for Inductor I= 28.3iE
I for Resistor I= 7E.

What I then did was sum the individual I values and let it equal the total value. But I didn't get anywhere with it. Am I getting somewhere?

 

[gneill]

Since it's a series circuit the current must be the same for all components. That'll be your E/Z value, where Z is the total impedance. That same current flows through each component and produces potentials across them.

Your value for I total is okay, but you might as well normalize the complex value (divide both terms by the 50.44 so you have a canonical form of complex number: a + ib). As it turns out, that complex number that you determined is also known as the admittance of the circuit. Admittance is the complex analog of conductance. Where G = 1/R for resistances, Y = 1/Z for impedances.

So if you calculate Y = 1/Z, then the current in the circuit is E*Y. That's Ohm's law in terms of admittance (conductance). And the potential across a component with impedance z is then E*Y*z. You can pick out the expression that represents the "multiplier" of E for the component's voltage.

 

[Michael 37]

I just realized that my individual I values were wrong. I multiplied E by the impedance instead of dividing by it.

To be perfectly honest I have no idea about the above message but I will try to follow what you are saying and see where I get. Is there not a formula that gives me voltage amplitude across a component or is it not that simple? Thanks again.

 

[gneill]

I*z is the give you the complex voltage across z. |I*z| is its amplitude.

 

[Michael 37]

Y=1/Z so Y = 1/7-1.2i. You then said potential is E*Y*z so my potential across my resistor is then :
= ((E)(7))/(7-2.1i)? I am struggling to find how I am going to get the amplitude across the resistor. Sorry for being slow at this but I can't see where we are going with this.

Thanks

 

[Michael 37]

Due to my severe lack of understanding of circuits as you have probably identified, do you think we should maybe move on to the other parts of the question and hopefully I will be capable of understanding how they work?

 

[gneill]

Y=1/Z so Y = 1/7-1.2i. You then said potential is E*Y*z so my potential across my resistor is then :
= ((E)(7))/(7-2.1i)? I am struggling to find how I am going to get the amplitude across the resistor. Sorry for being slow at this but I can't see where we are going with this.

Thanks

Sorry for the delay in getting back to you. I was taking advantage of the warm sunlight to make a few repairs on the roof...

Yes, the potential across the resistor is given by ((E)(7))/(7-2.1i). Put 7/(7 - 1.2i) into the standard form: a + bi. Then the potential across the resistor is (a + bi)E. E is currently an unknown quantity so you leave it as E. But you can take the magnitude of a + bi, right?

This is just a use of Ohm's law. You find the current through the circuit using Ohm's law with the total impedance and the source voltage E. Then you find the potential across an individual component using that current and the individual impedance of the component. The only complication is that you are working with complex values rather than real values, but the basic procedure is the same.

 

[gneill]

FYI, here's a diagram of the circuit under discussion, if that helps.