Gustav
- 57
- 5
- Homework Statement
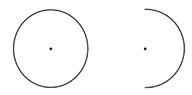
- Consider a circular ring with radius R and uniform longitudinal charge density λ as in the figure at the left, below.
a).Determine the electrostatic potential in the center of the circle.
b).Assume that a charge of magnitude q is in the center of the circle. The power of it then becomes zero, i.e. we have a state of equilibrium. Is this stable or unstable? Motivate the answer!
c)Assume now that we remove half of the ring and that the longitudinal charge density remains the same. the same, as in the figure at the right (The ring is not conductive.) Determine the magnitude of the force acting on the charge q.
d).We now let the figure on the right instead represent the cross section of a semi-circular cylinder, (which we may have obtained by dividing a cylinder length). The axis of the cylinder is perpendicular to the plan of the figure. The cylinder is very ("infinitely") long and has a surface charge density σ. Instead of the charge q represents the point in the figure now a straight line charge with longitudinal charge density λ_0. Determine the amount of the force per unit length acting on the line charge.
- Relevant Equations
- V = 1/4*pi*ε_0 ∫ λ*dl
∇* E =ρ /ε_0
F = Eq
I am unsure how to solve the problem and would appreciate any suggestens on how to start solving the problem.