Electrostatic potential of a circular ring

[KiNGGeexD]

I'm a little stumped with this problem, I have posted a photograph below as there is a diagram to compliment the question

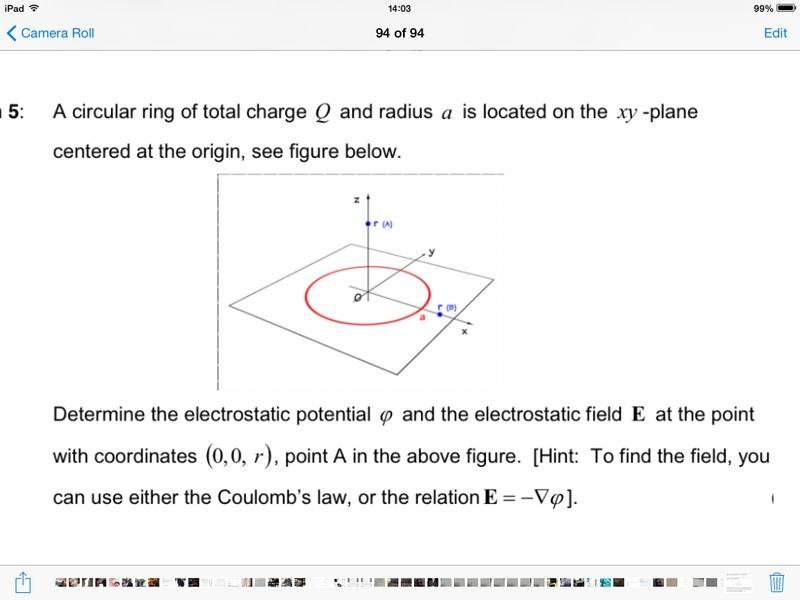Expressions which I used where

V(r)= k q/r

Where q= σ da

Where da is an element of area

And k= 1/4πεI messed around with these expressions for a while but it didn't really go anywhere I was having trouble defining and element of area (to use spherical coordinates or not).Any help or suggestions would be great thanks in advanced :):):):)

 

[nasu]

What area? It is a ring. You can consider linear charge density.

 

[KiNGGeexD]

Ok so area of the circle is

πr^2

And if I'm assuming linear charger density my equation would becomeV(r)= k λ/r dl

 

[nasu]

Do you realize that you will have to integrate over the ring? Have you done any similar problems?

 

[KiNGGeexD]

Yea I realize that but I haven't had a similar problem, most problems have been on the xy plane alone

 

[nasu]

Oh, just now I realized that your point A is on the z axis.
There is an "a" in the xy plane that misled me.

Then is is much simpler than I thought.
If you take a small element of ring with length dl, what will be the charge on this element?
What will be the distance between this element and the point A?

 

[KiNGGeexD]

What I mean is it was a two dimensional problem where lines were the only consideration rather than areas or volumes

 

[nasu]

Oh, here it's the same too. It has nothing to do with areas or volumes.

 

[KiNGGeexD]

The distance between the two points would be(z^2+ x^2)^1/2

 

[KiNGGeexD]

Would I just use my distance and integrate from -a to a, or rather multiply by 2 and integrate from 0 to a?

 

[Aryamaan Thakur]

Just one hint!
Distance between point A and any point on ring is constant (Pythagoras Theorem - hehe).
Take an element dq on the ring. You must know the expression of potential due to a point charge.
You'll get an integral. ∫ dq = Q
The answer will come in terms of total charge of ring.

 

[nasu]

The last post was from 2014.

 

[PeroK]

With any luck the OP has graduated by now.

 

[Aryamaan Thakur]

Not every single person in this world has graduated. Others might have the same query. Right?

 

[nasu]

So when you say "you" you mean a generic person (who did not graduate) and not the OP. :) It looked like you were answering the question the OP asked in April 2014, right above your answer.