gruba
- 203
- 1
Homework Statement
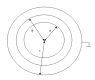
Three very long (theoretically infinite long) hollow cylindrical conductors, with radius a,b,c (c>b>a) are in vacuum. Inner and central conductor are charged, and outer conductor is grounded. Potentials of inner and central conductors with reference point relative to outer conductor are Va,Vb. Find longitudinal charge density of all three conductors.
Homework Equations
Electric field of cylindrical conductor can be derived using Gauss law for vacuum: E=Q'/(2πrε0), where Q' is longitudinal charge density.
Electric potential of cylindrical conductor is given by: V=∫Edl, where dl represents integration by radius.
The Attempt at a Solution
If outer conductor is grounded, and it is a referent point to potentials Va and Vb, integration for Va will be from (a to b)+(b to c),
Va=(Q'/(2πε0))*(ln(b/a)+ln(c/b))
Integration for Vb will be from (b to c),
Vb=(Q'/(2πε0))*ln(c/b)
We need to find longitudinal charge density for each capacitor, so for first we derive it from Va:
Q'=(2πε0Va)/(ln(b/a)+ln(c/b))
For second conductor, we derive it from Vb:
Q'=(2πε0Vb)/(ln(c/b))
Third conductor is grounded, so the potential of the third conductor is equal to zero, thus the longitudinal charge density of the third conductor is equal to zero.
Could someone check this, and help if something is not correct?
Thanks for replies.