Tanya Sharma
- 1,541
- 135
Homework Statement
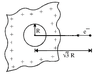
An infinite dielectric sheet having charge density σ has a hole of radius R in it. An electron is released on the axis of the hole at a distance R√3 from the centre. What will be the velocity which it crosses the plane of sheet? (e = charge on electron and m = mass of electron)
Homework Equations
The Attempt at a Solution
Force at a distance x on the axis of the hole can be calculated by finding electric field at a distance x .Electric field is found by superimposing the electric field due to the sheet and the circular disk containing charge density -σ .## E = \frac{σ}{2ε_0}\frac{x}{\sqrt{R^2+x^2}}##
##mv\frac{dv}{dx} = -\frac{σ}{2ε_0}\frac{x}{\sqrt{R^2+x^2}}##
##vdv = -\frac{σ}{2mε_0}\frac{x}{\sqrt{R^2+x^2}}dx##
Now integrating under proper limits I get ## v^2 = \frac{\sqrt{3}σe}{2mε_0}## which gives incorrect answer .
Is this the correct way to approach the problem ?
I would be grateful if somebody could help me with the problem.
Attachments
Last edited: