jisbon
- 475
- 30
- Homework Statement
- Bob has a mass of 50kg. He stands on a weighing scale inside an a elevator which moves up from stationary position. Reading on scale shows 60kg for first 10 seconds and 45kg for the next 20 seconds. Assuming g is 10m/s^2, what is displacement of elevator after 30 seconds?
- Relevant Equations
- Fnet= F-mg
F=ma
EDIT: As per @Orodruin 's suggestion(s), I have edited my problems and equations, sorry for the confusion as I typed this out hasty.
So from this question, I understand I have to find the net force for the first 10 seconds and deceleration for 20 seconds.
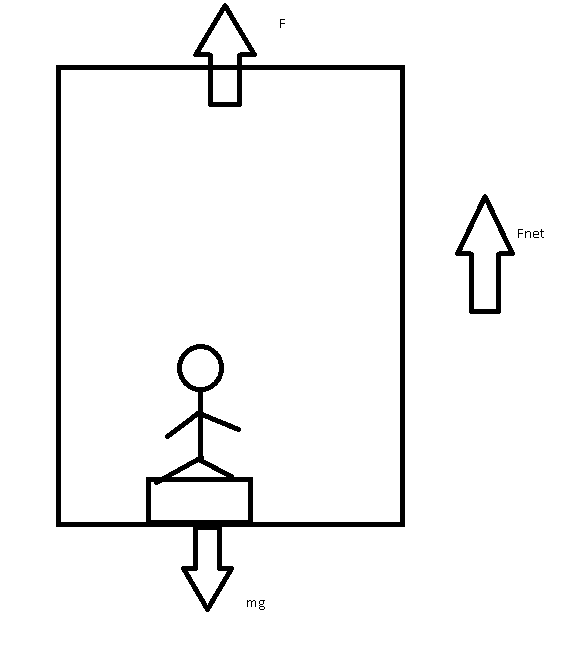
The scale shows the force with which the elevator acts on Bob, hence for first 10 seconds,
## F = 60kg * 10m/s^2= 600N##
##F_{net} = 600N- (50)(10) = 100N##
##Acc_{elevator 10seconds} = 100N/50kg = 2m/s^2##
##Velocity_{elevator 10seconds} = at = (2)(10) =20m/s##
On the other hand, for next twenty seconds
## F = 45kg * 10m/s^2= 450N##
##F_{net} = 450N- (50)(10) = -50N##
##Acc_{elevator 10seconds} = -50N/50kg = -1m/s^2##
Displacement = Displacement of first 10 seconds + Displacement of next 20 seconds
= ##(ut+\frac{1}{2}at^2) + (ut+\frac{1}{2}at^2)##
= ##(0(10)+\frac{1}{2}(2)10^2) + (20(20)+\frac{1}{2}(-1)20^2)##
= 300m
So from this question, I understand I have to find the net force for the first 10 seconds and deceleration for 20 seconds.
The scale shows the force with which the elevator acts on Bob, hence for first 10 seconds,
## F = 60kg * 10m/s^2= 600N##
##F_{net} = 600N- (50)(10) = 100N##
##Acc_{elevator 10seconds} = 100N/50kg = 2m/s^2##
##Velocity_{elevator 10seconds} = at = (2)(10) =20m/s##
On the other hand, for next twenty seconds
## F = 45kg * 10m/s^2= 450N##
##F_{net} = 450N- (50)(10) = -50N##
##Acc_{elevator 10seconds} = -50N/50kg = -1m/s^2##
Displacement = Displacement of first 10 seconds + Displacement of next 20 seconds
= ##(ut+\frac{1}{2}at^2) + (ut+\frac{1}{2}at^2)##
= ##(0(10)+\frac{1}{2}(2)10^2) + (20(20)+\frac{1}{2}(-1)20^2)##
= 300m
Last edited by a moderator: