EMF induced by a magnet falling through a coil

[zee123]

Homework Statement

How will the flux and emf graphs look like for a magnet that falls freely through a coil

Relevant Equations

E= -NBA/time taken , flux=BA

I've been told that if you drop a magnet through a coil the induced emf and flux graphs would look like this:

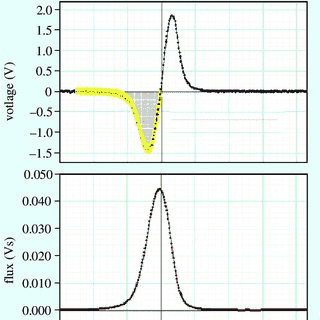
I understand that when the bar magnet is in the middle of the coil the emf induced is zero as flux change in top and bottom is in opposite directions but why is effective flux maximum when emf induced is zero, shouldn't the effective flux be zero as well? And, in the second half of the magnets jounery shouldn't the effective flux be negative as more of the flux linkage is contributed by the top half of the magnet when it is leaving the coil?

 

[Gordianus]

A better definition for the induced emf would be $E=-\frac{d\Phi}{dt}$. Check with this one.

 

[rsk]

Since,as Gordianus says, the emf depends on the rate of change of flux linkage, it can help to think of the emf graph as the gradient of the flux graph (but remembering the negative sign).

 

[kuruman]

Or you can view the bottom graph as the integral over time of the top graph (still remembering the negative sign).

 

[Steve4Physics]

I hope this might provide a bit of physical/geometrical insight, to complement the mathematical insights from the other answers.

Remember it is the rate of change of flux, not the amount flux, which determines the induced emf.

Look at these diagrams:

Fig. 1 shows the field (lines of flux) around a bar magnet. I haven’t put arrows on but you easily add them mentally if you want.

Fig. 2 shows only the lines of flux. Note each is actually a complete loop and each loop passes through the magnet.

Fig. 3 shows the lines of flux with the magnet just above the coil (sides of coil shown in red). Note there are only 2 lines of flux inside the coil. A small movement down will quickly increase this number, giving a large induced emf.

Fig. 4 shows the lines of flux with the magnet centred on the coil’s centre. There are now 8 lines of flux (maximum) inside the coil’s area. A small movement down will not change this number. So the induced emf = 0 even though the flux is maximum.

(As an additional note, if the there were a complete flux loop inside the coil it wouild have zero contribution to the net flux through the coil - because the upwards section cancels the downwards section.)

Hope that all makes sense.