Drop height of a magnet vs. induced EMF in a solenoid

[haruspex]

I calculated the x-int from the function values but the full plot looks like this:View attachment 301284
y-axis is in V, and x-axis is in m

Ok, that looks at least as good as the straight line fit you had in post #1, but we have thrown in an extra arbitrary parameter: the x intercept. So in terms of justifying a claim of parabolic behaviour, there is not enough data. You would need to rerun the experiment using smaller heights for the drop.
Unfortunately, that is just the domain in which the monopoles through solenoid model will diverge most clearly from both of @kuruman's simplified models.

 

[kuruman]

I interpreted your work as having considered two models: point dipole through solenoid length L; monopole pair separated by L through a single loop. The expected difference is that the monopoles will exhibit different magnitude positive and negative peaks because of the acceleration.
But do either of these match the data in post #1 better than the shown straight line fits? If not, can a monopole pair through a solenoid do better?

I guess I was not clear enough. I deserve only half the credit (or blame). My model is a point dipole falling through a solenoid of length $L$. The other model is not mine and consists of two monopoles separated by $L$ falling through a single loop. It is described here https://www.physicsforums.com/threads/calculating-magnetic-field-strength-of-a-magnet.1005917/page-5 post #123.

Unfortunately, that is just the domain in which the monopoles through solenoid model will diverge most clearly from both of @kuruman's simplified models.

Yes, my simplified model works if the magnet is released from a height such that the flux through the top loop of the solenoid is negligible. It will fail if the bar magnet is, say, halfway into the solenoid. According to my model, a point dipole has an estimated "sphere of influence" (SOI) of radius approximately equal to 3 solenoid radii. I think that the details of how a bar magnet can be modeled as an assembly of point dipoles become more significant when the magnet starts moving closer to the solenoid than farther away.

 

[kuruman]

I have additional thought to enhance my previous message #37 regarding the sphere of influence SOI of the falling dipole. Consider an observer at a fixed location $z'$ relative to the origin in the middle of the solenoid. The plot below shows the spatial profile of the emf contributed by the ring next to the observer when the dipole is at location $z$. The abscissa, $\frac{z'-z}{a}$ is the distance from the observer's ring to the dipole in units of the solenoid radius $a$. Apart from various constants. the spatial dependence of the emf is given by $$\frac{d\Phi}{dt}=\frac{\zeta}{\left(1+\zeta^2\right)^{5/2}}~~~~\left(\zeta \equiv \frac{z'-z}{a}\right).$$ This function has extrema at $\zeta=\pm\frac{1}{2}$ and is shown below. The vertical gridlines mark the extrema.

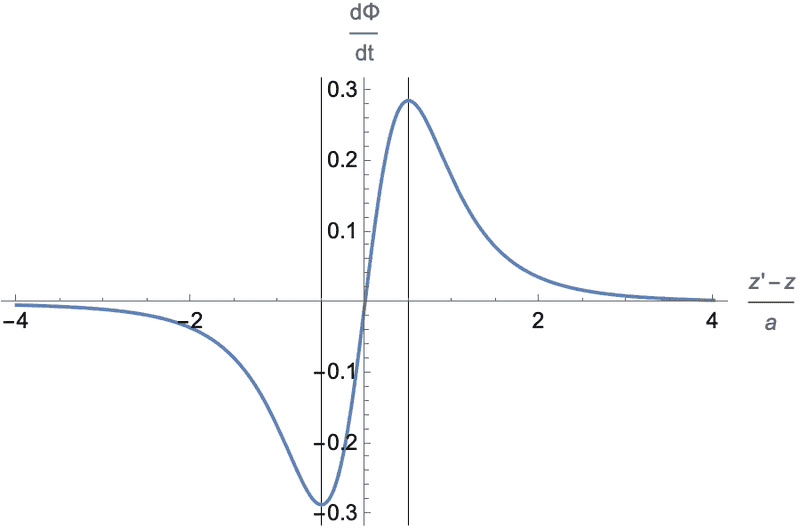
Note that the signal from the observer's ring is essentially zero when the dipole is farther than 2 solenoid diameters ($4a$) in either direction. That could be construed as defining the size of the SOI. The spatial profile can be viewed as voltage wave traveling down the solenoid with propagation speed $v=v_0+gt$.

Of course, the signal picked up by a voltmeter with one lead connected to the top ring and the other to the bottom ring would be the sum of all the voltage rises and drops but only from the rings that are within the SOI. Thus, when the SOI is completely within the solenoid, there will be equalizing positive and negative contributions and there is no signal. Only when the SOI is close to the exit end will there be a signal. This is where the length to diameter ratio of the solenoid become important to the profile of the signal. My guess is that with @billyt_ 's setup, when the trailing end of the SOI has just cleared the top of the solenoid, the leading end is about to exit. That's because one can see the curve flattening a bit at the inflection point. For comparison, I have appended below a calculation where the length of the solenoid is 3 SOI lengths. The middle is clearly flat.

My suggestion to @billyt_ , if he were to take additional measurements, is to start the magnet no closer than one solenoid diameter from the top and increase the height from there. Use the data to verify whether the falling magnetic dipole is good model for the asymptotic behavior. If it is, then he can worry about refinements.

Edited to fix typo.

 

[Charles Link]

The dipole model looks like it works fairly well, but an analytical result is possible that should be nearly exact. In post 25 the integral $\Phi_{solenoid}$ might prove difficult to evaluate, but the integral of $(d \Phi/dt)_{solenoid}=(N/S) \int\limits_{0}^{S} \frac{d \Phi(z+s)}{dt} \, ds$ is straightforward, because the result will be essentially the $\Phi$ that we started with, multiplied by $v(t)$. Evaluating the integral will give two terms for each monopole, for a total of 4 terms. It would be a lot of work to write out the 4 terms in Latex, but in any case, this approach should work. If the magnet has a substantial length to it, it could be advantageous to try this additional calculation.

 

[haruspex]

Evaluating the integral will give two terms for each monopole, for a total of 4 terms.

Yes, yes, I did all that days ago. My problem is finding the point in the descent that maximises the pdf. As I think you mentioned, the only way is likely numerical methods, so I need to plug in all the numeric data.

 

[Charles Link]

The physics of this problem for a magnet of substantial length, along with a solenoid, is really determined by the flux for a monopole formula, integrating the flux over the length of the solenoid. Fitting the voltage peaks to a curve in an empirical manner is semi-interesting, but there doesn't seem to be any real physics in that process for this case.

 

[haruspex]

The physics of this problem for a magnet of substantial length, along with a solenoid, is really determined by the flux for a monopole formula, integrating the flux over the length of the solenoid. Fitting the voltage peaks to a curve in an empirical manner is semi-interesting, but there doesn't seem to be any real physics in that process for this case.

I feel the thread has been instructive on the interplay between theory and experiment.

The stated purpose of the experiment was to study the relationship between drop height and peak voltage. The data appeared to show a good linear fit, but that was at odds with the parabola implied by simplified models. The question then was whether the experiment was flawed, the fit invalid, or the models too simple.

The plot in post #33 shows that the fit was quite possibly a fluke since just as good a fit could be obtained to a parabola. A next logical step would be to rerun the experiment but probing the region in which the difference between linear and parabolic would be more evident.