Drop height of a magnet vs. induced EMF in a solenoid

[billyt_]

Homework Statement

Attempting to determine a relationship between the height at which the magnet is dropped (relative to the centre of the solenoid) and the induced EMF in the solenoid.

Relevant Equations

$\varepsilon = -N \frac{d\Phi}{dt}$ $\Phi = B A \cos \theta$

I am currently working on an experiment that involves dropping a magnet from varying heights and measuring how the induced emf of a solenoid changes as a result. I am currently somewhat struggling with a derivation for a relationship between the two variables, however, this is what I have been thinking about so far:
- Making assumptions to make things easier: magnet maintains constant acceleration throughout the solenoid (doesnt really slow down), Magnet remains upright throughout the fall, so that theta = 0.
- The solenoid experiences the greatest magnitude of emf when it is somewhere in between one of the ends of the solenoid and the middle, where it is 0.

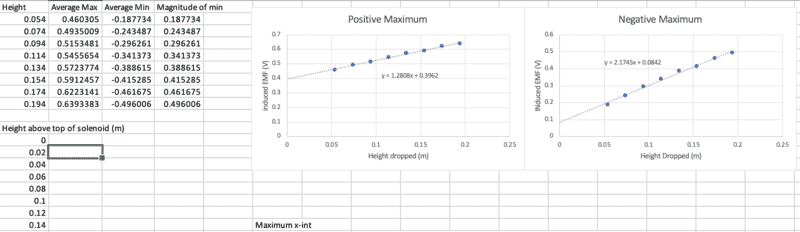
I have collected data, and strangely, it yielded a linear graph of emf magnitude vs. height dropped.

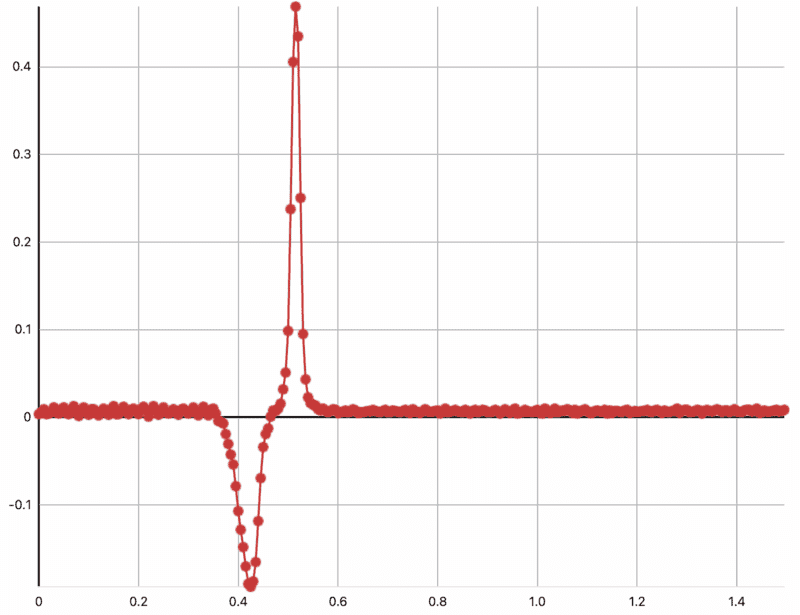
Here is also a graph of what one trial of dropping the magnet at 0cm above the top of solenoid (5.4cm above the centre) looks like (emf vs. time)

Thanks for any help!

 

[haruspex]

The EMF at an instant will depend on the velocity of the magnet, the strength of the horizontal component of the field, and how much of the coil is engaged by the field. The horizontal component of the field reaches peak magnitude at two different places, but at the later position the velocity is greater.
If you suppose the horizontal component of the field reaches peak engagement with the coil when length x of the magnet is within the coil, can you deduce x from the positions of the peaks in the second graph?

 

[kuruman]

I once did a calculation for the induced emf when a dipole falls through a single loop. I was interested in finding an expression for the force on the magnet due to the induced magnetic dipole in the loop. I calculated the spatial profile of the emf to be $$\frac{d\Phi}{dt}=\frac{3\mu_0ma^2(z'-z)\dot z}{2[(z'-z)^2+a^2]^{5/2}}$$where
$m=$ the moment of the point magnetic dipole
$a=$ the radius of the loop
$z' =$ the position of the loop
$z =$ the position of the dipole.
I defined dimensionless parameter $\zeta\equiv \dfrac{z'-z}{a}$ which is the distance between the loop and the dipole in units of one loop radius and plotted omitting the constants. The plot is shown below.

I have defined dimensionless independent variable $\zeta=\dfrac{z'-z}{a}$ to do the plot. It is the distance between the loop and the falling dipole in unts of the radius $a$. The plot shows that $\frac{d\Phi}{dt}$ starts becoming appreciable when the dipole is to within about 3 radii away from the loop.

All this is, of course, an idealization because the data for this study were collected using a permanent magnet of finite extent, not a point dipole which doesn't exist. Nevertheless, I think it is fair to say that when the magnet is dropped through a solenoid, only the loops that are "in range" are engaged.

 

[billyt_]

Yes, I have been able to work out the bounds within which the emf is induced, however, I am struggling to figure out a relationship that directly related h, the height at which the magnet is dropped, and the rate of change of flux. To do this I would have to somehow fit the variable inside the faraday's law, because the emf is definitely increasing as I am increasing the height. Or would I actually incorporate height into the formula for flux, and then find a relationship with the emf.

 

[kuruman]

Yes, I have been able to work out the bounds within which the emf is induced, however, I am struggling to figure out a relationship that directly related h, the height at which the magnet is dropped, and the rate of change of flux. To do this I would have to somehow fit the variable inside the faraday's law, because the emf is definitely increasing as I am increasing the height. Or would I actually incorporate height into the formula for flux, and then find a relationship with the emf.

I think you need to write an equation of motion and solve it to find the distance of the magnet as a function of time. Measuring the area under the positive and negative peaks in the $\mathcal{E}$ vs. $t$ curve might be useful. It represents the change in magnetic flux over a time interval. That's because if you multiply both sides of Faraday's law by $dt$ and integrate (ignoring the negative sign), you get $$\int_{t_1}^{t_2} \mathcal{E}dt=\int_{t_1}^{t_2} d\Phi= \Phi(t_2)-\Phi(t_1).$$ If you choose points in time $t_1$ and $t_2$ when the magnet is, respectively, well above and well below the ends of the solenoid, $\Phi(t_2)=\Phi(t_1)=0.$ The idea that the areas under the positive and negative curves are equal explains, at least qualitatively, why the right peak is skinnier and taller than the right peak. If you think of the peaks roughly as triangles of equal areas, the triangle with the smaller base will have the larger height. The reason for this asymmetry is because the emf is proportional to the velocity. The increasing velocity squeezes the time axis as one moves to the right on the graph. The proportionality to the velocity is a direct consequence of Faraday's law and the chain rule of differentiation. If one writes the magnetic flux as a function of some generic spatial variable $x(t)$, then $$\frac{d\Phi(x(t))}{dt}=\frac{d\Phi}{dx}\frac{dx}{dt}=\frac{d\Phi}{dx}\dot x.$$As mentioned earlier, I have derived the retarding magnetic force on a point dipole (not a magnet) and the expression I got is $${F}=\frac{ 9 a^4 (z'-z)^2 \mu _0^2 m^2}{4 R \left[a^2+(z'-z)^2\right]^5}\dot z.$$Here $R$ is the resistance of the coil which is needed to find the induced current. The rest of the symbols are as defined in post #3. Assuming mass M for the dipole, the differential equation to solve would be $$M\ddot{z}=-\frac{ 9 a^4 (z'-z) ^2 \mu _0^2 m^2}{4 R \left[a^2+(z'-z) ^2\right]^5}\dot z+Mg.$$I have assumed that "down" is positive. Of course you have a solenoid of $N$ turns while the equation is for a single loop. You will have to consider a superposition of contributions from coils equally distributed in the interval $z'_1 \leq z' \leq z'_2$.

It is not an easy problem.

 

[haruspex]

I think you need to write an equation of motion and solve it to find the distance of the magnet as a function of time. Measuring the area under the positive and negative peaks in the $\mathcal{E}$ vs. $t$ curve might be useful. It represents the change in magnetic flux over a time interval. That's because if you multiply both sides of Faraday's law by $dt$ and integrate (ignoring the negative sign), you get $$\int_{t_1}^{t_2} \mathcal{E}dt=\int_{t_1}^{t_2} d\Phi= \Phi(t_2)-\Phi(t_1).$$ If you choose points in time $t_1$ and $t_2$ when the magnet is, respectively, well above and well below the ends of the solenoid, $\Phi(t_2)=\Phi(t_1)=0.$ The idea that the areas under the positive and negative curves are equal explains, at least qualitatively, why the right peak is skinnier and taller than the right peak. If you think of the peaks roughly as triangles of equal areas, the triangle with the smaller base will have the larger height. The reason for this asymmetry is because the emf is proportional to the velocity. The increasing velocity squeezes the time axis as one moves to the right on the graph. The proportionality to the velocity is a direct consequence of Faraday's law and the chain rule of differentiation. If one writes the magnetic flux as a function of some generic spatial variable $x(t)$, then $$\frac{d\Phi(x(t))}{dt}=\frac{d\Phi}{dx}\frac{dx}{dt}=\frac{d\Phi}{dx}\dot x.$$As mentioned earlier, I have derived the retarding magnetic force on a point dipole (not a magnet) and the expression I got is $${F}=\frac{ 9 a^4 (z'-z)^2 \mu _0^2 m^2}{4 R \left[a^2+(z'-z)^2\right]^5}\dot z.$$Here $R$ is the resistance of the coil which is needed to find the induced current. The rest of the symbols are as defined in post #3. Assuming mass M for the dipole, the differential equation to solve would be $$M\ddot{z}=-\frac{ 9 a^4 (z'-z) ^2 \mu _0^2 m^2}{4 R \left[a^2+(z'-z) ^2\right]^5}\dot z+Mg.$$I have assumed that "down" is positive. Of course you have a solenoid of $N$ turns while the equation is for a single loop. You will have to consider a superposition of contributions from coils equally distributed in the interval $z'_1 \leq z' \leq z'_2$.

It is not an easy problem.

I'm not convinced the retardation of the magnet will be that significant. If there is no circuit, how does conservation of work operate here?

A more obvious concern is the claimed linear fit of peak voltage against height dropped. In a crude model - single loop of coil, only engaged as the most effective part of the field moves through it - one would expect (retardation apart) the peak velocity to vary as the square root of the height dropped. Of course, that gets smeared as we allow for multiple loops to be engaged by multiple parts of the field simultaneously.
Indeed, the right hand graph in post #1 does give a hint of a declining gradient.

 

[kuruman]

I'm not convinced the retardation of the magnet will be that significant. If there is no circuit, how does conservation of work operate here?

It may not be significant in this particular setup but it could be significant as demonstrated here.



Conservation of work operates when one considers that some of the power put in the falling magnet by gravity appears as heat dissipated through $I^2R$ losses in the solenoid.

I tried to estimate if there is retardation in @billyt_'s setup as follows. We are told that

Here is also a graph of what one trial of dropping the magnet at 0cm above the top of solenoid (5.4cm above the centre) looks like (emf vs. time)

If the magnet were in free fall without retardation over the length of twice the distance to the centre (= 10.8 cm), the time of flight would be (to 2 sig figs) $$t_{\!f}=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\times 0.108~\text{m}}{9.8~\text{m/s}^2}}=0.15~\text{s}.$$
In the figure below I have superimposed the 0.15 s interval assuming that the vertical gridline labels are in seconds. I think it is clear that it takes longer than 0.15 s for the magnet to drop through the solenoid. It's not much, but it's there.

On edit:
After additional thoughts and calculations, I disavow my approach shown in this post.

 

[haruspex]

some of the power put in the falling magnet by gravity appears as heat dissipated through I2R losses in the solenoid.

But I stated "if no circuit". Can the current be enough to matter?

 

[kuruman]

But I stated "if no circuit". Can the current be enough to matter?

I guess not. I thought of the solenoid as a "discrete" tube, but it isn't. I shall have to go back to the drawing board and see if I can modify the equation I have for a single loop to accommodate a solenoid of $N$ loops and finite length $L$.

 

[kuruman]

I think I have an equation that reproduces the features of the graph posted by OP. I considered a point dipole falling through a solenoid of $N$ turns, length $L$ and radius $a$. I put the origin of coordinates at $\frac{L}{2}$ and assumed that the dipole is dropped through the solenoid starting from rest at position $h+\frac{l}{2}.$ I used the kinematic equation $z(t)=h+\frac{L}{2}-\frac{1}{2}gt^2$ for the position of the dipole on the $z$-axis. Then
I calculated the magnetic flux through a circle of radius $a$ at position $z'$ when the dipole is at $z$ using $\Phi=\int \mathbf{B}_{dipole} \cdot \mathbf{\hat n}~dA$ to get $$\Phi ( z')=\frac{ \mu _0 m a^2}{2 \left[a^2+(z'-z) ^2\right]^{3/2}}$$where $a$ is the radius of the solenoid, and $m$ the dipole moment. This gives $$\frac{\text{d$\Phi $}}{\text{dt}}=\frac{3 \mu _0 m a^2 (z'-z) ~ \dot{z}}{2 \left[a^2+(z'-z)^2\right]^{5/2}}.$$ Now a stack of solenoid loops of height $dz'$ contains $\frac{N}{L}dz'$ loops so that the emf at the ends of the stack is $$d(\text{emf})=\frac{N}{L}\frac{3 \mu _0 m a^2 (z'-z) ~ \dot{z}}{2 \left[a^2+(z'-z)^2\right]^{5/2}}dz'.$$We add all the contributions to get the emf at the two ends of the solenoid, $$\text{emf}=\frac{3N\mu_0ma^2~\dot z}{2L}\int_{L/2}^{-L/2}\frac{ (z'-z) }{ \left[a^2+(z'-z)^2\right]^{5/2}}dz'.$$ With $z(t)$ as assumed above, the integral yields $$\text{emf} (t)
=\frac{4N \mu _0 m a^2 g}{L} \left[\frac{t}{\left(4 a^2+\left(2 (h+L)-g t^2\right)^2\right)^{3/2}}-\frac{t}{\left(4 a^2+\left(2 h-g t^2\right)^2\right)^{3/2}}\right]$$Of course what counts is the expression in the square brackets as the product of constants up front is just a scaling parameter. I chose realistic values as best as I could ascertain from the OP, L = 0.1 m, a = 0.02 m. The latter was a guess that made the plots look like the one posted by the OP. Below are the plots for 3 values of h = 0.5 m (blue), 0.7 m (orange) and 0.1 m (green).

There is qualitative agreement with the experimental results:

• In each plot the negative peaks are fatter and shorter than the positive peaks.
• The peaks increase as the height from which the dipole is dropped is increased.
• There is a hint of a plateau at the inflection point.
• The overall signal spans approximately the same time interval of about 0.2 s as the data.

 

[haruspex]

0.1 m (green).

Did you mean 1.0m? Or should the others be 0.05m, 0.07m?
In this analysis, there is no retardation, right?

The next step would be to model the first pair of charts, finding how peak emf depends on drop height. Working from your equation, I got up to terms of order $t^{32}$ before giving up.

 

[kuruman]

Did you mean 1.0m? Or should the others be 0.05m, 0.07m?
In this analysis, there is no retardation, right?

The next step would be to model the first pair of charts, finding how peak emf depends on drop height. Working from your equation, I got up to terms of order $t^{32}$ before giving up.

I meant 0.1 m for the length of the solenoid and 0.05 m, 0.07 m and 0.1 m for the drop heights. The length of the solenoid as given by OP is 10.8 cm. Sorry about the confusion. I finished this late at night and I was tired. Yes, there is no retardation. That is implicit in the equation for $z(t)$ where the acceleration is just -$g$.

I have some ideas about working on the equation to explore the peak vs. height dependence that do not involve an expansion. I admire your tenacity for going up to t³².

 

[kuruman]

Success! First I replotted emf(t) vs t with vertical gridlines added at the times when the dipole crosses the top, the middle and the end of the solenoid. I was thrilled to see the plot below which makes great sense in retrospect.

If we consider a sphere of radius about one solenoid diameter centered at the dipole, the flux will change most rapidly when the sphere is halfway in the top or halfway out the bottom and hardly at all in the middle. Thus, the peak extrema occur at the times when the dipole enters and exits the solenoid. The times are $t_1=\sqrt{\frac{2h}{g}}$ and $t_2=\sqrt{\frac{2(h+L)}{g}}.$ These can be substituted in the equation to find the extrema
$$\begin{align} & P_1=\text{emf} (t_1)=\frac{4N \mu _0 m a^2 g}{L} \frac{1}{4} \sqrt{\frac{h}{2 g}} \left(\frac{1}{\left(a^2+L^2\right)^{3/2}}-\frac{1}{a^3}\right)=K \sqrt{h} \nonumber \\ & P_2=\text{emf} (t_2)=\frac{4N \mu _0 m a^2 g}{L} \frac{1}{4} \sqrt{\frac{h+L}{2 g}} \left(\frac{1}{\left(a^2+L^2\right)^{3/2}}-\frac{1}{a^3}\right)=K\sqrt{h+L}\nonumber \end{align}$$It follows that $$P_2^2-P_1^2=\text{const.}$$which is testable hypothesis. The plot below shows the difference of the squares of the peaks plotted against the dropping height $h$ (discrete points). The red line is the average of the data. Lacking experimental uncertainty information, I added error bars as ± one standard deviation. Except for one outlier, it looks like the data support the theory.

 

[haruspex]

Success! First I replotted emf(t) vs t with vertical gridlines added at the times when the dipole crosses the top, the middle and the end of the solenoid. I was thrilled to see the plot below which makes great sense in retrospect.
View attachment 301210
If we consider a sphere of radius about one solenoid diameter centered at the dipole, the flux will change most rapidly when the sphere is halfway in the top or halfway out the bottom and hardly at all in the middle. Thus, the peak extrema occur at the times when the dipole enters and exits the solenoid. The times are $t_1=\sqrt{\frac{2h}{g}}$ and $t_2=\sqrt{\frac{2(h+L)}{g}}.$ These can be substituted in the equation to find the extrema
$$\begin{align} & P_1=\text{emf} (t_1)=\frac{4N \mu _0 m a^2 g}{L} \frac{1}{4} \sqrt{\frac{h}{2 g}} \left(\frac{1}{\left(a^2+L^2\right)^{3/2}}-\frac{1}{a^3}\right)=K \sqrt{h} \nonumber \\ & P_2=\text{emf} (t_2)=\frac{4N \mu _0 m a^2 g}{L} \frac{1}{4} \sqrt{\frac{h+L}{2 g}} \left(\frac{1}{\left(a^2+L^2\right)^{3/2}}-\frac{1}{a^3}\right)=K\sqrt{h+L}\nonumber \end{align}$$It follows that $$P_2^2-P_1^2=\text{const.}$$which is testable hypothesis. The plot below shows the difference of the squares of the peaks plotted against the dropping height $h$ (discrete points). The red line is the average of the data. Lacking experimental uncertainty information, I added error bars as ± one standard deviation. Except for one outlier, it looks like the data support the theory.

View attachment 301214

Ok, so your more complete model supports the $\sqrt h$ relationship I had for the single coil model in post #6. But it is unclear how to map the h in your model to that used in the plots in post #1.
I had thought we should be able to find a constant adjustment that would give a reasonable fit to the graphs, E.g. take the best straight line fits to $V^2$ against h and see where they intercept the X axis. But the plots in post #1 look worryingly straight already, so I feel we would need to abandon the dipole model to get a more realistic answer. It gets complicated because we would need a model for the shape of the field lines from a bar magnet. We might also need to consider the (unknown) gap between magnet and solenoid.

@billyt_ has perhaps lost interest, leaving it as just an academic discussion between us (with you doing the heavy lifting).

 

[kuruman]

But it is unclear how to map the h in your model to that used in the plots in post #1.

You probably missed this in post #1

Here is also a graph of what one trial of dropping the magnet at 0cm above the top of solenoid (5.4cm above the centre) looks like (emf vs. time)

So the mapping between his "Height" and my "h" is $h=\text{Height}-0.054$. That explains the odd entries under "Height" which really are $h$ in increments of 20 cm.

If this is to be continued, I think we will need to know the radius the solenoid or at least the length-to-radius ratio.

 

[haruspex]

You probably missed this in post #1

So the mapping between his "Height" and my "h" is $h=\text{Height}-0.054$. That explains the odd entries under "Height" which really are $h$ in increments of 20 cm.

No, I mean that for a bar magnet the most 'effective' field line in this context is not at the end of the bar but some way into it.

 

[billyt_]

Hi, I am definitely still interested, as this is a project that I am still working on, just was quite busy over the weekend. It's going to take me a bit to digest the maths above but from what I have scanned I agree with you — I think emf should be proportional to the root of the height, as the velocity will be proportional to the rate of change of flux.

- Also I am not able to find any proper sources anywhere that have previously conducted this experiment or attempted to relate these variables so I am very thankful for the help.

This is also a photograph of the experiment set-up:

 

[Charles Link]

See https://www.physicsforums.com/threa...radays-law-of-induction.1012796/#post-6605131
including post 3:
See https://www.physicsforums.com/threads/calculating-magnetic-field-strength-of-a-magnet.1005917/page-5
especially posts 122-123.
We already treated this same experiment in-depth. Looks like similar derivations have been repeated above.

Edit: Perhaps the latest post is somewhat different if the OP is doing it for the case of a solenoid.

 

[haruspex]

: Perhaps the latest post is somewhat different if the OP is doing it for the case of a solenoid.

I have been trying to explain why the first two graphs in post #1 look so straight, rather than as parabolas centred on the x axis. I suspect it is to do with the fact that this is a solenoid, not just one loop.
If the magnet were to pass through at constant velocity then the peak magnitudes would appear at a certain pair of depths. Since it is accelerating, the peaks will be a little delayed. Since the velocity should rise as the sqrt of the height descended, the delay (in terms of height at which it occurs) will be greater for the shorter drop heights (lower velocities). That will increase the peak voltages at low drop heights in comparison to the peak voltages at greater drop heights.
Maybe that is enough to explain the flattening.

 

[Charles Link]

I have been trying to explain why the first two graphs in post #1 look so straight, rather than as parabolas centred on the x axis. I suspect it is to do with the fact that this is a solenoid, not just one loop.
If the magnet were to pass through at constant velocity then the peak magnitudes would appear at a certain pair of depths. Since it is accelerating, the peaks will be a little delayed. Since the velocity should rise as the sqrt of the height descended, the delay (in terms of height at which it occurs) will be greater for the shorter drop heights (lower velocities). That will increase the peak voltages at low drop heights in comparison to the peak voltages at greater drop heights.
Maybe that is enough to explain the flattening.

The solenoid can be solved in reasonably closed form with an integral, using the results of a single ring. Numerical integration of it might be necessary, but I don't have the programming tools to do that on my computer, and it really would be some extra work. In any case, I do recommend everyone take a look at the second "link" in post 18. This problem has basically been solved, and @hutchphd had a very good solution there. Besides posts 122-123 of that "link", see also posts 137,138, and 139.

 

[haruspex]

The solenoid can be solved in reasonably closed form with an integral, using the results of a single ring. Numerical integration of it might be necessary, but I don't have the programming tools to do that on my computer, and it really would be some extra work. In any case, I do recommend everyone take a look at the second "link" in post 18. This problem has basically been solved, and @hutchphd had a very good solution there.

I looked at that link, but isn't it only for a single loop? And doesn’t it imply that the peak pdf should vary as the square root of the drop height?
Yes, a closed form can be got for the solenoid, but then we have to find the point in the descent at which the pdf peaks and hence the value of the peak for a given drop height.

 

[Charles Link]

I looked at that link, but isn't it only for a single loop? And doesn’t it imply that the peak pdf should vary as the square root of the drop height?
Yes, a closed form can be got for the solenoid, but then we have to find the point in the descent at which the pdf peaks and hence the value of the peak for a given drop height.

Yes, it would take a little work to go from a single loop to a solenoid. I think I would recommend to the OP that he first experiment with a coil that can be treated the same as a single loop, before going to a solenoid. I need to look it over more carefully, but I do believe the case of different drop heights was basically treated in the thread that I gave the "link" to, by considering $z=z_o+v_o t+(1/2)gt^2$.
Using $v^2=v_o^2+2gd$, I think that will tell you basically what the peak EMF is, because it will be proportional to the velocity, at least for a single ring.

 

[haruspex]

I do believe the case of different drop heights was basically treated in the thread that I gave the "link" to, by considering $z=z_o+v_o t+(1/2)gt^2$.
Using $v^2=v_o^2+2gd$, I think that will tell you basically what the peak EMF is, because it will be proportional to the velocity, at least for a single ring.

Sure, but the issue to be resolved is why the data plotted in post #1 of this thread does not appear to conform to that analysis. As a function of drop height, it looks too linear.

 

[billyt_]

Sure, but the issue to be resolved is why the data plotted in post #1 of this thread does not appear to conform to that analysis. As a function of drop height, it looks too linear.

It is interesting, as just from some simple graphical analysis, it appears that the function of negative magnitude vs. height looks a lot closer to a $y = \sqrt{x}$ function than the positive magnitude.

Using the experimental data, if we try to plot it as a power function on excel, the equations below can be seen, although the positive maximum graph is quite clearly pushing it a bit. Also note that error bars can't really fix this as the experimental uncertainty I obtained is all less than 0.01 Volts.

 

[Charles Link]

I think the theoretical result for a somewhat long solenoid is rather difficult to compute, and we can't expect the peak amplitude to behave anything like it does for a single ring or a bundle of rings that span a short distance.

If we were to actually go and proceed with a numerical evaluation of the integral of a solenoid composed of a distribution of single rings, I think we would likely find the results agree very closely with the experiment.

@haruspex , @billyt_ The integral that is needed is to take the result of post 123 for the link that I listed, (second "link" of post 18 above), and replace $z$ by $z+s$, and perform the integral $\Phi_{solenoid}(z)=(N/S)\int\limits_{0}^{S} \Phi(z+s) \, ds$, where $S$ is the length of the solenoid. This really is somewhat simple to do numerically, but I don't have that kind of computational capability on this Chromebook. (and see also post 120 by @hutchphd of this thread. That is a very important one that spells out the whole idea. See also posts 137, 138, and 139).

 

[haruspex]

It is interesting, as just from some simple graphical analysis, it appears that the function of negative magnitude vs. height looks a lot closer to a $y = \sqrt{x}$ function than the positive magnitude.

Using the experimental data, if we try to plot it as a power function on excel, the equations below can be seen, although the positive maximum graph is quite clearly pushing it a bit. Also note that error bars can't really fix this as the experimental uncertainty I obtained is all less than 0.01 Volts.
View attachment 301278

You must not assume it starts at the origin of your coordinates. You do not know what the 'effective' drop height is. Find the best fit of the form $y^2=Ax+B$, for each separately.

 

[haruspex]

The integral that is needed

Let me try to be really clear. Integrating for the solenoid case for a given velocity and pair of positions of the monopoles is not the problem; that's easy. Assuming some constant separation of the monopoles , that gives $V=V(v, x)$, where v is the instantaneous velocity and x the instantaneous position.
If h is the drop height then $v=v(h,x)$. We can presume this is $v^2=2g(h-x)$.
The problem is to find max V wrt x as a function of h. That would appear to involve solving for x in $\frac{\partial V}{\partial x}=0$.

 

[Charles Link]

Let me try to be really clear. Integrating for the solenoid case for a given velocity and pair of positions of the monopoles is not the problem; that's easy. Assuming some constant separation of the monopoles , that gives $V=V(v, x)$, where v is the instantaneous velocity and x the instantaneous position.
If h is the drop height then $v=v(h,x)$. We can presume this is $v^2=2g(h-x)$.
The problem is to find max V wrt x as a function of h. That would appear to involve solving for x in $\frac{\partial V}{\partial x}=0$.

The solution I am proposing is to simply evaluate $V$ vs. $t$ numerically (for each drop height $h$), and read from the graph the approximate peak. With a solenoid, the complete analytical solution for $V_{max}$ is much too complex. The integral that I listed in post 25 looks next to impossible to try to get a result in closed form. It needs to be evaluated numerically, and that should be fairly routine.

 

[kuruman]

The solution I am proposing is to simply evaluate $V$ vs. $t$ numerically (for each height $h$), and read from the graph the approximate peak.

In post #13 I have expressions for the peaks. They are based on the equation for $emf(t)$ in post #10. In that equation $L$ is the length of the solenoid. It gives an identical plot (to within an overall multiplicative constant) to the one for the falling monopoles with the same $L$ as the separation between them.

 

[Charles Link]

In post #13 I have expressions for the peaks. They are based on the equation for $emf(t)$ in post #10. In that equation $L$ is the length of the solenoid. It gives an identical plot (to within an overall multiplicative constant) to the one for the falling monopoles with the same $L$ as the separation between them.

Very good @kuruman Looking at your calculations, it looks like they are in agreement with the "link" that I posted, and it looks like you were able to take it a step further by getting a result by evaluating the integral over the solenoid. :)

Suggestion would be to include both a magnet $L$ with opposite poles, and a solenoid length $S$. I think this will make for 4 terms in the numerical computation of $V(t)$, rather than the two that you show in post 10.

Edit: I need to study this in more detail. The calculations by @kuruman in post 10 use a dipole, while in the thread whose "link" I provided, the calculations use a monopole. In any case, it looks like $d \Phi/dt$ can be integrated over the length of the solenoid for the monopole, even though the integral of $\Phi$ over the length of the solenoid is much more difficult.

Edit 2: It looks as if the dipole result integrates over the length of the solenoid using $d \Phi /dt$, and with a second try I think I got the same success with the monopole result of post 123 of the thread whose "link" I provided. This seems to make it so that the complete system of a magnet of finite length $L$ and a solenoid of length $S$ can be solved in the simple form of 4 terms that that I mentioned above. I think the result will be just slightly different from @kuruman 's terms though, but fairly similar.

 

[billyt_]

You must not assume it starts at the origin of your coordinates. You do not know what the 'effective' drop height is. Find the best fit of the form $y^2=Ax+B$, for each separately.

When plotted to a custom fit, we obtain an equation of $y = \sqrt{1.465x + 0.03263}$. This would suggest that if the magnet were to be dropped at ~2 cm below the top of the horizontal, no emf would be induced. However, for this plot we do notice a relatively poor RMSE value, but at the moment I think this is a more accurate plot for the obtained data. (the values used here are for the first negative peak, as we will see less peak "delay" due to the acceleration as the dipole passes through the solenoid).

Edit: the x-intercept actually comes out to be 2.2cm which is 0.5cm before the magnet would pass through the midpoint between the top and the centre.

 

[haruspex]

When plotted to a custom fit, we obtain an equation of $y = \sqrt{1.465x + 0.03263}$. This would suggest that if the magnet were to be dropped at ~2 cm below the top of the horizontal, no emf would be induced. However, for this plot we do notice a relatively poor RMSE value, but at the moment I think this is a more accurate plot for the obtained data. (the values used here are for the first negative peak, as we will see less peak "delay" due to the acceleration as the dipole passes through the solenoid).

View attachment 301282

Edit: the x-intercept actually comes out to be 2.2cm which is 0.5cm before the magnet would pass through the midpoint between the top and the centre.

You don't show the y values in that plot. Looks like the x-axis is somewhere lower down since the curve should be vertical where it crosses that axis.

 

[billyt_]

You don't show the y values in that plot. Looks like the x-axis is somewhere lower down since the curve should be vertical where it crosses that axis.

I calculated the x-int from the function values but the full plot looks like this:

y-axis is in V, and x-axis is in m

 

[Charles Link]

Be sure and see a couple additions I made to post 30. I think @kuruman has some very good calculations in post 10 above.

 

[haruspex]

In post #13 I have expressions for the peaks. They are based on the equation for $emf(t)$ in post #10. In that equation $L$ is the length of the solenoid. It gives an identical plot (to within an overall multiplicative constant) to the one for the falling monopoles with the same $L$ as the separation between them.

I interpreted your work as having considered two models: point dipole through solenoid length L; monopole pair separated by L through a single loop. The expected difference is that the monopoles will exhibit different magnitude positive and negative peaks because of the acceleration.
But do either of these match the data in post #1 better than the shown straight line fits? If not, can a monopole pair through a solenoid do better?