SUMMARY
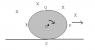
The discussion centers on the calculation of electromotive force (emf) induced in a rotating disk, specifically addressing the formula BvR. Participants confirm that when considering a rod PS rotating about the center O, the induced emf due to rotation is zero. This conclusion is reached by analyzing the velocity components of the rod and recognizing that the contributions from different segments of the rod cancel each other out. The participants agree that the total induced emf across the rod can be expressed as the sum of the emf due to translation and the emf due to rotation.
PREREQUISITES
- Understanding of electromagnetic induction principles
- Familiarity with the concepts of rotation and translation in physics
- Knowledge of the formula for induced emf, specifically BvR
- Basic grasp of vector components and their application in physics
NEXT STEPS
- Study the derivation of the formula for induced emf in rotating systems
- Learn about the principles of electromagnetic induction in different geometries
- Explore the effects of angular velocity on induced emf in rotating disks
- Investigate the application of Faraday's Law in complex motion scenarios
USEFUL FOR
Students of physics, educators teaching electromagnetism, and engineers working with rotating machinery or electromagnetic systems will benefit from this discussion.
 til tomorrow)
til tomorrow)