- #1
Jahnavi
- 848
- 102
Homework Statement
Homework Equations
The Attempt at a Solution
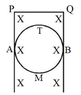
First I will label a few points .
A is the point on the ring touching the rails , vertically below P .
B is the point on the ring touching the rails , vertically below Q .
T is the topmost point on the ring .
M is the bottommost point on the ring .
When speed of the ring is v , EMF induced between A and B will be Bv(2r) with B at higher potential. But there will be no net EMF induced in the ring as there is no change in flux .This means we can treat the two half rings as if EMF 2Bvr is induced in top half rings ATB and also EMF 2Bvr is induced in bottom half ring AMB .
Now I will write KVL in the ring in anticlockwise sense starting from A -> M -> B -> T ->A . Suppose i1 current flows through AMB and i2 current flows in ATB .Resistance of the two parts will be R/2 each .
Writing KVL in the loop of the ring , 2Bvr -i1R/2 -2Bvr + i2R/2 = 0
This gives i1 = i2 . That means current flows from A to B via M and also flows from A to B via T . It is like there are two resistances R/2 in parallel between A and B .
We also have i1=i2= 4Bvr/R .
Current flowing in PQ will be ( i1+ i2 )= 8Bvr/R from Q to P i.e option 4) . Is that correct ?
Is my work and more importantly my reasoning alright ?
Attachments
Last edited: