designroad
- 7
- 0
Summary: I set it up my investigation as in the image with two independent variables: the mass of ball 1 and the angle of ramp inclination. I released ball 1 and started a timer when it stuck ball 2 then stopped it at the end of the track. I then took the average velocity of ball 2 over the 1 metre horizontal track.
I need some help in deriving a formula which links mass of ball 1 and angle of inclination, to the velocity of ball 2. Any help/guidance would be much appreciated. Thank you :-)
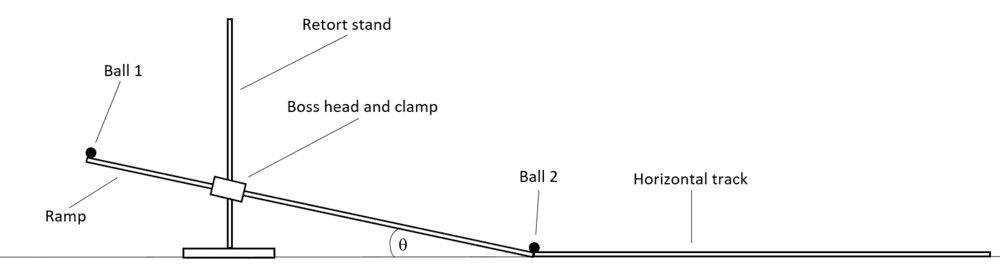
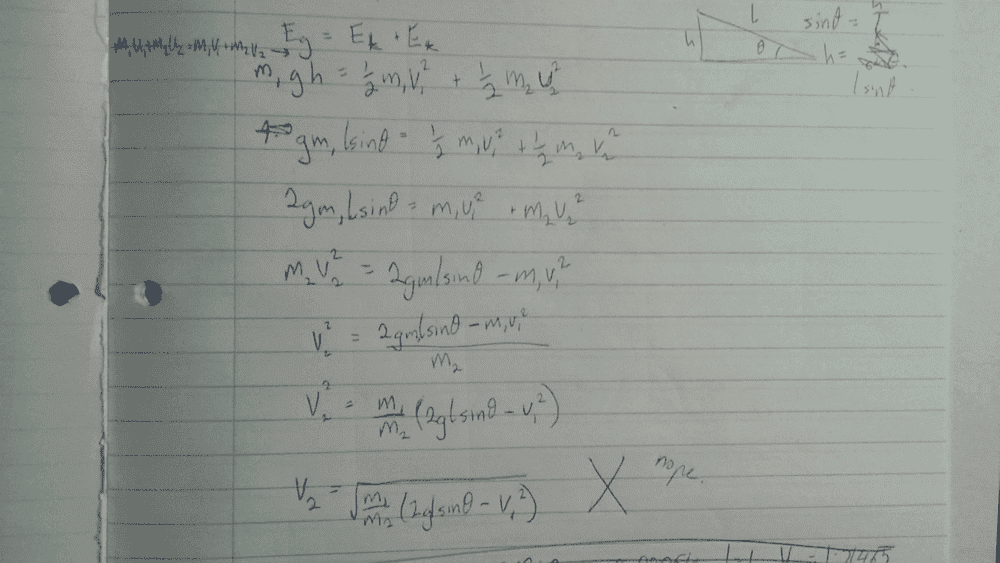
I need some help in deriving a formula which links mass of ball 1 and angle of inclination, to the velocity of ball 2. Any help/guidance would be much appreciated. Thank you :-)