Energy dissipated through resistor

[hopkinmn]

Homework Statement

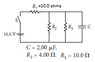
The problem first asks to find potential difference across the capacitor after the switch has been closed a long time. Then it asks to determine the energy stored in a capacitor when the switch has been closed for a long time. I got both these answers right, with Vcapacitor=2.22V and Energy in capacitor=4.9284*10^-6 Joules.

The last part asks to determine how much energy has dissipated through R3 after the switch has been opened.

Homework Equations

The Attempt at a Solution

I know that Power(P)=Current(I)*Voltage(V)=(delta charge)/(delta time)*V and that Power is the derivative of Energy. However, no charge is provided and no time is provided (we just know that it's been a long time), so I'm not sure how to go about solving this problem.

The right answer for the energy dissipated through R3 is 1.41*10^-6 Joules

 

[gneill]

There are several related expressions for the (instantaneous) power dissipated in a resistor. One involves the current through the resistor, the other the voltage across the resistor.

If you can write the equation for the voltage across the resistor w.r.t. time, then you'll be in a position to use one of those expressions for the power.

 

[hopkinmn]

So I set up the expression P(t)=V(t)^2/R3, where V(t)=V*e^(-t/(R3*C))
When I integrate this expression, I get E(t)=-.5*V^2*C*e^(-2t/(R3*C))
Since the switch has just been opened, t=0.
I then get E(0)=-.5*V^2*C
But this just gives me the same answer for part B, where I found energy stored in the capacitor when the switch has been closed for a long time. I'm not sure what I'm doing wrong.

 

[gneill]

So I set up the expression P(t)=V(t)^2/R3, where V(t)=V*e^(-t/(R3*C))
When I integrate this expression, I get E(t)=-.5*V^2*C*e^(-2t/(R3*C))
Since the switch has just been opened, t=0.
I then get E(0)=-.5*V^2*C
But this just gives me the same answer for part B, where I found energy stored in the capacitor when the switch has been closed for a long time. I'm not sure what I'm doing wrong.

One small problem. When the capacitor discharges it does so through both resistors R2 and R3. So the time constant must reflect that.

 

[hopkinmn]

Ok, I understand it now, thanks so much!