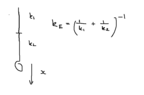Energy stored in a double spring system

[sdfsfasdfasf]

Homework Statement

Find out how much energy is stored in the system.

Relevant Equations

x

Part c) i) is no problem, clearly k/m = w^2 = (2pi f)^2, solving for k using f = 0.15, m=6.6 x 10^5 gives k=5.9 x 10^5 which is close to 6x10^5.
Part ii) is causing me some issues however. Clearly the model uses two springs, of combined spring constant 6 x 10^5, therefore the spring constant of either spring is 12 x 10^5 (in series spring constants add like capacitance in series, so we have 2/k = k(effective)). The energy stored by the each spring will be 1/2(12 x 10^5)(0.71)^2, leading to a total energy of (12 x 10^5) (0.71)^2. The official solution is 1/2 (6 x 10^5)(0.71)^2 which is clearly 4 times smaller than my answer. Where did I go wrong?

 

[Orodruin]

The springs are not in series. The moving mass mass is in between the springs. Compressibg one string stretches the other.

 

[sdfsfasdfasf]

Could you explain further please?
Both springs store energy, right?

 

[sdfsfasdfasf]

Could you explain further please?
Both springs store energy, right?

Each spring will store (1/2)(k)(0.71)^2 , meaning the total stored is k(0.71)^2, but how to work out k?

 

[kuruman]

Where did I go wrong?

The problem states that $k$ is the spring constant of the combination. That means treat it as if it were a single spring, i.e. it is the effective spring constant.

 

[sdfsfasdfasf]

The problem states that $k$ is the spring constant of the combination. That means treat it as if it were a single spring, i.e. it is the effective spring constant.

I would be happy doing that if the spring was extended from either the left or the right. However the spring is clearly being extended in the middle (hence one spring is being compressed and one extended).

If it looked like this then I would be fine.

 

[Orodruin]

Again: The springs are not in series. The mass is in between the springs

 

[sdfsfasdfasf]

Ok. I have done some googling and found out that the effective spring constant is the sum of the individual ones rather than the harmonic thing I was doing before. This however does not indicate that they are in parallel, right? Is there an intuitive reason as to why the constants add.

 

[kuruman]

I would be happy doing that if the spring was extended from either the left or the right. However the spring is clearly being extended in the middle (hence one spring is being compressed and one extended).

If it looked like this then I would be fine.
View attachment 340280

You are missing the point. The spring constant that you calculated is that of the combination, i.e. of an equivalent spring. In other words, replace the two springs with a single spring that has the spring constant that you calculated and such that the given mass oscillates with the given frequency.

It looks like this

 

[sdfsfasdfasf]

So the mass need not be in the middle anymore?

 

[kuruman]

So the mass need not be in the middle anymore?

Not if you consider the equivalent situation.

 

[sdfsfasdfasf]

And it turns out this new spring has a constant which is the sum of the old ones not the reciprocal of the sum of the reciprocals. Do you have any more reading info on this? How am I meant to know all this information if my spec only covers basic situations in the book :(

 

[Orodruin]

Ok. I have done some googling and found out that the effective spring constant is the sum of the individual ones rather than the harmonic thing I was doing before. This however does not indicate that they are in parallel, right? Is there an intuitive reason as to why the constants add.

They are very much in parallel. Consider what would be the difference in terms of forces and energy if you changed the side one of the springs is on.

Also consider what @kuruman is saying: You do not need to consider anything as a combination of springs because you have the effective spring constant of the system as a whole. You can just use that.

You are missing the point. The spring constant that you calculated is that of the combination, i.e. of an equivalent spring. In other words, replace the two springs with a single spring that has the spring constant that you calculated and such that the given mass oscillates with the given frequency.

It looks like this

View attachment 340281

Just to add that while I completely agree that this is the simplest solution, I think it is still instructive to understand why the two springs that the OP assumed are actually in parallel.

 

[kuruman]

How am I meant to know all this information if my spec only covers basic situations in the book :(

See post #5. You did not grasp the significance of "where k is the spring constant of the combination" in the statement of the problem.

 

[kuruman]

Just to add that while I completely agree that this is the simplest solution, I think it is still instructive to understand why the two springs that the OP assumed are actually in parallel.

I agree. It would be instructive to OP to derive equivalent parallel and series spring combinations from Newton's second law.

 

[sdfsfasdfasf]

How was I meant to know that if we have the effective spring constant that the mass is at the end

 

[Orodruin]

How was I meant to know that if we have the effective spring constant that the mass is at the end

This is the definition of the effective spring constant. It is the constant k of a spring to which the mass is attached to one end such that the force on the mass is given by F = -kx where x is the displacement.

 

[haruspex]

How was I meant to know that if we have the effective spring constant that the mass is at the end

"effective" means you don't have to worry about why the spring constant of the combination has that value, it just does.

As regards "parallel" versus "series" in the context of springs, the real distinction is whether a displacement x of the load implies a length change of x in all the springs (parallel) or is shared somehow amongst the springs (series). Or, in terms of forces, whether the net force F on the load implies that force on all the springs (series) or is distributed across them (parallel). Note the reversal.
In the arrangement given here, both views would classify them as parallel.