Engineering Statics - Moments problem

[yugeci]

Homework Statement

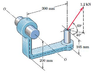
I have attached the diagram. The question says "Compute the Moment Mo of the 1.2kN force about the axis O-O.

Homework Equations

M = r x F
AB = OB - OA
Resolving forces, Fx = F cos Θ.. Fy = F sin Θ etc.

The Attempt at a Solution

Here are the axes I've made, using the Right Hand Rule:

OA = (-300, 0, 105)
OB = (0, 0, 200)

So AB = (300, 0, 95) .. this is the r vector.

For the F vector, Fz = 1.2 sin 60 = 1.04 kN
Fxy = 1.2 cos 60 = 0.6 kN

Fx = -0.6 cos 50 = -0.39 kN
Fy = 0.6 sin 50 = 0.46 kN

M = r x F (since we need the moment about the O-O axis, I'll just get the j component).

| 300 0 95 |
| -0.39 0.46 1.04 |

Solving gives M @ o-o as -349.05 Nm. However the answer is +327 Nm. What have I done wrong?

 

[BvU]

I am missing why the y-component of the r-vector should be zero...
[Edit] sorry, axes mixed up. Will re-do.

 

[BvU]

Turns out you also have something mixed up (means we're even...):

The r-vector is BA, not AB, so (-300, 0, -95)​

Doesn't help us to find a different value, though. Checked a few times.

So have some confidence in your result (and tell me what we did wrong once you find out ).

 

[yugeci]

It turns out that we are right, I think. The original question (older edition) was in lb-in, and I guess there was some error when the values got converted to N-mm. You are right that we need the BA vector instead of AB.. but that's just a sign change.. which leads me to my next question?

When do we use AB, and when do we use BA (the reverse)? Here are two example questions:

In the first we use BA. In the second we use AB.

Thanks in advance.

 

[yugeci]

Help? :\

 

[BvU]

The word "on" is key here!

Antenna case:
On point B a force pulls in the direction BA. (So that force will have a positive z-component, positive y, negative x). But on point A the cable to B exercises a force that is in the direction AB (so all components opposite sign).
Can't say i like the picture very much, because the y-coordinate of B is pretty vague.
Does the exercise continue with something that involves assuming that on point A the sum of forces has no x- and y-components?

Turnbuckle case :
On point A which is part of member AD a force pulls in the direction AB. (So that force will have a negative z-component, positive x, positive y)

Help? :\

was out of town & off line in the weekend. Happens ;-)

PS Generally: nice pictures!

PS strings, rubber bands, springs, ropes, cables: in simple cases they are supposed to exercise longitudinal (in line, as opposed to transversal, perpendicular to..) forces (otherwise the ends would move sideways).
The forces on a string, cable, section of string, etc. point outwards, the forces the string, cable, etc. exercises on the stuff attached point "inwards". If the rope itself is weightless AND is not accelerated, all are equal in magnitude.