baby_1
- 159
- 16
Hello,
For a motor, we need to calculate the traveled distance and proper timing for its motion. Here is the trapzodial motion of our motor( we need that our motor traveled 20 degree in 2 seconds). (where t2=2t1)
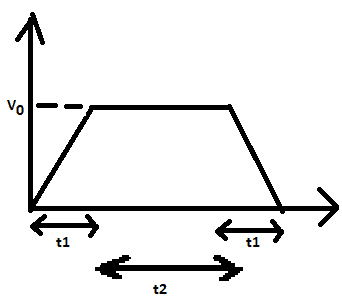
we know that the traveled distance is surface of our velocity diagram. So:
\frac{1}{2}at_{1}+V_{0}t_{2}+\frac{1}{2}at_{1}=\Theta_{T}=>(V_{0}=at_{1},t_{2}=2t_{1} )=>t_{1}=\sqrt{\frac{\Theta_{T}}{3a}}
for having t1=.5s @ theta=20 degree-> a=27.
by solving this equation we find t1=.49 and t2=.99 which seems be correct.
However, By calculating this equation for theta=90 degree (a=27) =>t1=1.29, t2=2.58. I calculated traveled distance:
\Theta_{1}=\frac{1}{2}at_{1}=22.46 degree
V=at=>V_{0}=at_{1}=> \Theta_{2}=V_{0}t_{2}=at_{1}t_{2}=89.9 degree
\Theta_{3}=\frac{1}{2}at_{1}=22.46 degree
\Theta_{1}+\Theta_{2}+\Theta_{3}>90
what is my mistake?
For a motor, we need to calculate the traveled distance and proper timing for its motion. Here is the trapzodial motion of our motor( we need that our motor traveled 20 degree in 2 seconds). (where t2=2t1)
we know that the traveled distance is surface of our velocity diagram. So:
\frac{1}{2}at_{1}+V_{0}t_{2}+\frac{1}{2}at_{1}=\Theta_{T}=>(V_{0}=at_{1},t_{2}=2t_{1} )=>t_{1}=\sqrt{\frac{\Theta_{T}}{3a}}
for having t1=.5s @ theta=20 degree-> a=27.
by solving this equation we find t1=.49 and t2=.99 which seems be correct.
However, By calculating this equation for theta=90 degree (a=27) =>t1=1.29, t2=2.58. I calculated traveled distance:
\Theta_{1}=\frac{1}{2}at_{1}=22.46 degree
V=at=>V_{0}=at_{1}=> \Theta_{2}=V_{0}t_{2}=at_{1}t_{2}=89.9 degree
\Theta_{3}=\frac{1}{2}at_{1}=22.46 degree
\Theta_{1}+\Theta_{2}+\Theta_{3}>90
what is my mistake?