Equation of motion and normal modes of a coupled oscillator

In summary, the conversation is about finding the amplitude and frequency of a simple oscillator with the equation of motion x(t) = Acos(ωt + φ). The individual is looking for help in understanding the equation and finding the amplitude. They have identified the frequency as √(k/m) and the equation of motion as a differential equation involving gravity and the spring's restoring force.
  • #1
VapeL
1
0
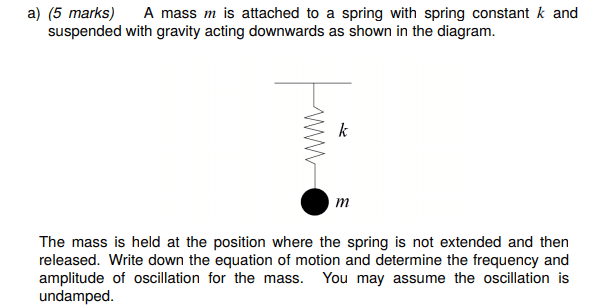
Homework Statement
Find the equation of motion of a mass on a spring
Relevant Equations
x(t) = Acos(ωt + φ)
This is a question from an exercise I don't have the answers to.

I have been trying to figure this out for a long time and don't know what to do after writing

mx''¨(t)=−kx(t)+mg
I figure that the frequency ω=√(k/m) since the mg term is constant and the kx term is the only term that changes.

I have the equation of motion written as x(t) = Acos(ωt + φ) but do not know how to go about finding the amplitude either.

Any help would be great thanks!

ePwCA.png
 
Physics news on Phys.org
  • #2
It looks like this is a simple (not coupled) oscillator.

It also looks like you have this backwards, in a sense. The equation of motion is not the expression for ##x## as a function of time, but rather it is Newton's second law, involving gravity and the restoring force that the spring exerts on the mass. In other words: It is a differential equation.
 

1. What is the equation of motion for a coupled oscillator system?

The equation of motion for a coupled oscillator system is a set of differential equations that describe the motion of two or more oscillators that are connected or coupled to each other. It takes into account the forces acting on each oscillator and their respective masses and positions.

2. How do you find the normal modes of a coupled oscillator system?

To find the normal modes of a coupled oscillator system, you can use the eigenvalue problem method. This involves solving for the eigenvalues and eigenvectors of the system's equations of motion. The eigenvectors represent the normal modes of oscillation, and the corresponding eigenvalues determine the frequencies of these modes.

3. What is the significance of normal modes in a coupled oscillator system?

The normal modes of a coupled oscillator system represent the independent modes of oscillation that the system can exhibit. Each normal mode has a specific frequency and amplitude of oscillation. By understanding the normal modes, we can predict the behavior of the system and how it will respond to different external forces or perturbations.

4. Can the normal modes of a coupled oscillator system be coupled?

Yes, the normal modes of a coupled oscillator system can also be coupled. This means that the oscillators are not completely independent and their motions are affected by each other. In this case, the normal modes will have a combination of frequencies and amplitudes from the individual oscillators.

5. How can the equation of motion and normal modes of a coupled oscillator system be applied in real-world systems?

The equation of motion and normal modes of a coupled oscillator system have many applications in various fields such as physics, engineering, and biology. They can be used to study the behavior of complex systems, such as molecules and atoms, and to design and optimize mechanical and electrical systems. They are also important in understanding the dynamics of biological systems, such as the human body and ecosystems.

Similar threads

Normal modes of four coupled oscillating masses (Kleppner and Kolenkow)
    • Introductory Physics Homework Help
Replies
4
Views
742
Coupled oscillators -- period of normal modes
    • Introductory Physics Homework Help
Replies
11
Views
1K
Finding the Oscillations of Pendulum A
    • Introductory Physics Homework Help
Replies
16
Views
1K
Max amplitude of a diving board that will not toss a pebble off?
    • Introductory Physics Homework Help
2
Replies
39
Views
2K
Getting the equations of motion for this SHM problem
    • Introductory Physics Homework Help
Replies
8
Views
1K
Kinematics, curvilinear motion (a couple of questions)
    • Introductory Physics Homework Help
Replies
30
Views
510
I Error tolerant normal mode frequency
    • Classical Physics
Replies
7
Views
1K
How to solve a differential equation for a mass-spring oscillator?
    • Introductory Physics Homework Help
Replies
2
Views
1K
Oscillating horizontal mass attached to a spring with Friction
    • Introductory Physics Homework Help
Replies
1
Views
2K
How Do Coupled Adiabatic Pendula Behave?
    • Introductory Physics Homework Help
Replies
1
Views
849

Hot Threads

Recent Insights

Back
Top