davidwinth
- 103
- 8
- TL;DR
- I want to find an equation of motion for the following system through the use of the Lagrangian approach.
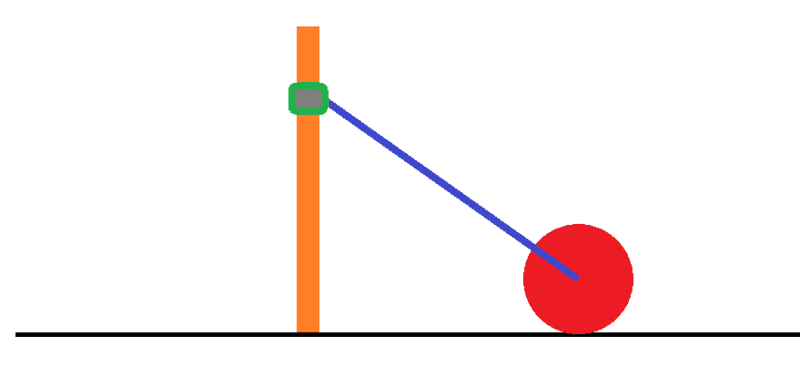
The system is shown below. It consists of a rod of length ##L## and mass ##m_b## connecting a disk of radius ##R## and mass ##m_d## to a collar of mass ##m_c## which is in turn free to slide without friction on a vertical and rigid pole. The disk rolls without slipping on the floor. The ends of the rod are attached such that they rotate without friction. I choose the angle ##\theta## between the horizontal and the rod as the generalized coordinate.The velocity of the center of mass of the collar is strictly vertical, and is given by: ##V{_c} = Lcos(\theta)\dot{\theta}##.
The velocity of the center of mass of the disk is strictly horizontal, and is given by ##V{_d}=-Lsin(\theta)\dot{\theta}##.
The translational velocity of the center of mass of the rod is obtained from its components as: ##V_{b} = \sqrt{\dot{x}_{b}^2 + \dot{y}_{b}^2} = \frac{L\dot{\theta}}{2}##.
The rotational velocity of the disk about its center of mass is given as: ##\omega_d = \frac{-Lsin(\theta)\dot{\theta}}{R}##.
The rotational velocity of the rod about its center of mass is given as: ##\omega_b = \dot{\theta}##.
Thus, the total kinetic energy for this system is the sum of all these contributions:
$$\frac{1}{2}m_{c}(Lcos(\theta)\dot{\theta})^2 + \frac{1}{2}m_{b}\left(\frac{L\dot{\theta}}{2}\right)^2 + \frac{1}{2}m_{d}\left(Lsin(\theta)\dot{\theta}\right)^2 + \frac{1}{2}I_{d}\left(\frac{Lsin(\theta)\dot{\theta}}{R}\right)^2 + \frac{1}{2}I_{b}(\dot{\theta})^2$$
Where the ##I_d## and ##I_b## are the moment of inertia about the centroid of the disk and rod, respectively.
My doubt is whether I have correctly accounted for the motion of the rod by decomposing it this way. Is there something I have neglected in considering the motion of the rod?
The velocity of the center of mass of the disk is strictly horizontal, and is given by ##V{_d}=-Lsin(\theta)\dot{\theta}##.
The translational velocity of the center of mass of the rod is obtained from its components as: ##V_{b} = \sqrt{\dot{x}_{b}^2 + \dot{y}_{b}^2} = \frac{L\dot{\theta}}{2}##.
The rotational velocity of the disk about its center of mass is given as: ##\omega_d = \frac{-Lsin(\theta)\dot{\theta}}{R}##.
The rotational velocity of the rod about its center of mass is given as: ##\omega_b = \dot{\theta}##.
Thus, the total kinetic energy for this system is the sum of all these contributions:
$$\frac{1}{2}m_{c}(Lcos(\theta)\dot{\theta})^2 + \frac{1}{2}m_{b}\left(\frac{L\dot{\theta}}{2}\right)^2 + \frac{1}{2}m_{d}\left(Lsin(\theta)\dot{\theta}\right)^2 + \frac{1}{2}I_{d}\left(\frac{Lsin(\theta)\dot{\theta}}{R}\right)^2 + \frac{1}{2}I_{b}(\dot{\theta})^2$$
Where the ##I_d## and ##I_b## are the moment of inertia about the centroid of the disk and rod, respectively.
My doubt is whether I have correctly accounted for the motion of the rod by decomposing it this way. Is there something I have neglected in considering the motion of the rod?