Solving for the Motion of a Spring Pendulum

[erobz]

Given the pendulum setup below:

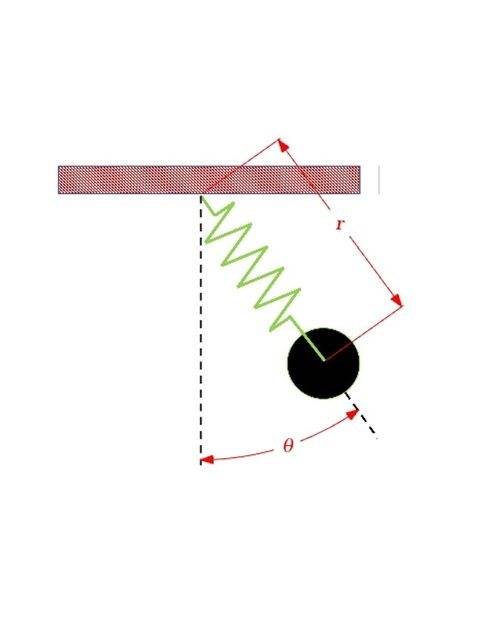
Details:

$m$ is the mass of the bob
$r$ is the instantaneous length of the spring
$\theta$ is the angle the bob makes w.r.t vertical
$I$ is the bobs mass moment of inertia about pivot
$l_o$ is the free length of the spring.
$k$ is the spring constant

The spring is assumed not to deflect laterally and is ideally massless. It is elevated to the angle $\theta$ at its free length without stretching and released. Summing torques about the piviot $\circlearrowright ^+$ I arrive at:

$$ r m g \sin \theta = I \ddot \theta \tag{1}$$

Next shift frame of reference to the mass and apply Newtons Second ( non-inertial frame) in the direction of $r$ with $\searrow ^+$

$$ m \ddot r = mg \cos \theta -k\left( r - l_o \right) + mr {\dot \theta}^2 \tag{2}$$

I've never really gone further with solving a system like this. What I was thinking of doing was solving $(2)$ first treating $\theta$ and $\dot \theta$ as parameters such that $(2)$ becomes:

$$ \ddot r + \left( \frac{k}{m} - {\dot \theta}^2 \right) r = g\cos \theta +\frac{k l_o}{m}$$

where I solve for $r$ as a second order ODE with constant coefficients, in other words solve$(2)$ as:

$$ \ddot r + \beta r = \kappa $$

Then use that result to numerically solve $(1)$ for $\ddot \theta$ with a small time step where I assume it is constant over that small interval.

Is that nonsense?

EDIT:

$(1)$ should be:

$$ r^2 \ddot \theta + 2 r \dot r \dot \theta + rg \sin \theta = 0 \tag{1}$$

 

[Baluncore]

Is that nonsense?

There is probably no one solution to the system.

Approaching the system from a different direction: Looking at the simplest model, I see two oscillators, the swing and the spring, that have independent natural frequencies. The pendulum bob mass will therefore move in an endless radial Lissajous figure.

But because the length of the pendulum will change the natural period of the swing, and the swing will change the vertical force, changing the length of the spring, the oscillators are coupled in a way that will phase lock to some longer period.

Neither oscillator will show its exact independent natural period, but those natural periods will be pulled slightly, until they are at an integer ratio to each other, repeating over a longer period. The radial Lissajous figure, described by the bob mass, will therefore be stable over that longer repetition period.

Just what that integer ratio will be will depend on the trajectory followed to the (initial) phase lock that is stable. There will be a whole field of stable lock integer ratio peaks available, separated by transitional saddles of differing depth.

Since for a specified swing angle, the coupling between the oscillators will be well-defined, it would be interesting to numerically simulate the model, to plot that field surface.

As energy is lost, the swing amplitude will reduce over time, so oscillator coupling will then change. How will the oscillators then transition to peaks with different integer ratios?

 

[erobz]

There is probably no one solution to the system.

It sounds like you are saying that the actual solution to the model above is not going to instantaneously return to its initial conditions on the other side of the datum, how does that happen? I'm not stretching the spring before release. Surely energy must be conserved, just like in its "rigid" pendulum counterpart. Why does it not just return to its initial state at $-\theta$?

I was thinking it would be some type of elliptical shape trajectory, you are saying its (excuse my ignorance) "semi" chaotic?

Its more than possible you've already explained it, and I'm not making the proper connections in your reply to understand it.

 

[Baluncore]

What is the natural period of the spring and mass?
What is the natural period of the swinging bob?
If they differ by a significant amount, it will not repeat a simple ellipse like pattern, but some more complicated pattern.
https://en.wikipedia.org/wiki/Lissajous_curve

 

[Baluncore]

Why does it not just return to its initial state at −θ?

Because the length of the spring will change during the first swing. At the end of the swing, the asynchronous spring period may still have non-zero dr/dt, so energy in the spring will prevent the pendulum from quite reaching −θ.

 

[erobz]

Motion prediction/understanding aside... Is the "solution technique" I concocted going to produce a reasonable curve, or do you think it is going to fall flat on its face rather quickly?

$$ \ddot r + \beta r = \kappa \tag{2}$$

As a recap I was thinking I could solve $(2)$ as a second order ODE with "constant" coefficients and initial conditions such that $r_{t+\Delta t} = f( \beta_t, \kappa_t,t)$

Where:

$$\beta_t = \left( \frac{k}{m} - {\dot \theta_t}^2 \right)$$
$$\kappa_t = g\cos \theta_t +\frac{k l_o}{m}$$

then in $(1)$ use $r = r_{t+\Delta t}$ and $I = I_{t+\Delta t}$ to numerically integrate:

$$ \frac{\Delta \omega}{\Delta t} = \frac{ r_{t+\Delta t} mg \sin \left( \theta_{t+\Delta t }\right)}{I_{t+\Delta t}} $$

Sorry if my notation is non-standard, difficult to interpret.

 

[erobz]

Because the length of the spring will change during the first swing. At the end of the swing, the asynchronous spring period may still have non-zero dr/dt, so energy in the spring will prevent the pendulum from quite reaching −θ.

Ok, I obviously didn't see that coming.

 

[Vanadium 50]

This seems to be a problem made for Lagrangian mechanics. Write down T-U in terms of generalized coordinates (which might not be the angle and length, but that would be my first stab at it) get the equations of motion, and diagonalize: at this point it's like any other coupled oscillator problem.

When done, set the spring constant to infinity and ensure you recover a simple pendulum, and set the swing amplitude to zero and ensure you recover a vertical spring.

 

[erobz]

This seems to be a problem made for Lagrangian mechanics. Right down T-U in terms of generalized coordinates (which might not be the angle and length, but that would be my first stab at it) get the equations of motion, and diagonalize: at this point it's like any other coupled oscillator problem.

When done, set the spring constant to infinity and ensure you recover a simple pendulum, and set the swing amplitude to zero and ensure you recover a vertical spring.

You overestimate me!

Anyhow, I think I have the equations of motion. Would the Lagrangian be helpful in some way there that I don't realize?

The daigonalizing bit... I'm assuming you are talking about diagonalizing the system of non-linear ODE's, after linearization? I wouldn't even know where to begin on that.

 

[hutchphd]

Anyhow, I think I have the equations of motion. Would the Lagrangian be helpful in some way there that I don't realize?

Give Wikipedia a look elastic pendulum
This is a nice problem on many levels IMHO.

 

[erobz]

Give Wikipedia a look elastic pendulum
This is a nice problem on many levels IMHO.

Yeah, it doesn't look like I have the equations correct... That hurts. apparenly there must be a torque component I missed involving $\dot x \dot \theta$

 

[TSny]

Yeah, it doesn't look like I have the equations correct... apparenly there must be a torque component I missed involving $\dot x \dot \theta$

Summing torques about the piviot $\circlearrowright ^+$ I arrive at:

$$ r m g \sin \theta = I \ddot \theta \tag{1}$$

The torque equation is $\tau = \dot L$, where $L = mr^2 \dot \theta$ is the angular momentum.
Note that $\dot L \neq I \ddot \theta$.

 

[hutchphd]

There is a rather extensive paper in Physica D but access probably an issue
https://doi.org/10.1016/j.physd.2019.132256

​

 

[erobz]

The torque equation is $\tau = \dot L$, where $L = mr^2 \dot \theta$ is the angular momentum.
Note that $\dot L \neq I \ddot \theta$.

Oh my!...all this time (an entire decade to be exact...shameful) I've been operating under the delusion that $r$ is fixed, and $\sum \tau = I \alpha$

Moving forward: that's the definition for the angular momentum of a point mass? I take it the full definition is actually:

$$ \sum \tau = \dot L = \dot I \dot \theta + I \ddot \theta $$

 

[TSny]

I take it the full definition is actually:

$$ \sum \tau = \dot L = \dot I \dot \theta + I \ddot \theta $$

Yes, with $I = mr^2$.

For a point mass, the angular momentum is defined as $\vec L = \vec r \times \vec p$. For motion in a plane and using polar coordinates, this gives $L = mr^2 \dot \theta$.

 

[bob012345]

Oh my!...all this time (an entire decade to be exact...shameful) I've been operating under the delusion that $r$ is fixed, and $\sum \tau = I \alpha$

Moving forward: that's the definition for the angular momentum of a point mass? I take it the full definition is actually:

$$ \sum \tau = \dot L = \dot I \dot \theta + I \ddot \theta $$

Probably for all the problems you have dealt with $r$ has been fixed. And $m$ as well. I only mentioned that as one might think of a swinging pendulum bob dripping paint to make a pattern.

 

[bob012345]

Give Wikipedia a look elastic pendulum
This is a nice problem on many levels IMHO.

I think the notation on this Wikipedia page is very confusing. They use $x$ and $y$ axis labels but write the equations in terms of $x$ and $\theta$. I think they mean the variable $x$ as displacement along the spring what is called $r$ in this thread.

 

[erobz]

Probably for all the problems you have dealt with $r$ has been fixed. And $m$ as well. I only mentioned that as one might think of a swinging pendulum bob dripping paint to make a pattern.

That's probably just about true (I may have been doing them incorrectly for years), but it is still disheartening to have graduated with a mechanical engineering degree and not realize this.

 

[hutchphd]

That's probably just about true (I may have been doing them incorrectly for years), but it is still disheartening to have graduated with a mechanical engineering degree and not realize this.

And of course you can't do the prototypical angular momentum example (spinning ice skater) without the $\dot I \dot {\theta}$ term !

 

[erobz]

Yes, with $I = mr^2$.

For a point mass, the angular momentum is defined as $\vec L = \vec r \times \vec p$. For motion in a plane and using polar coordinates, this gives $L = mr^2 \dot \theta$.

At the risk of making a fool of myself I'm now not certain if the $\dot I$ is technically correct?

$$ \mathbf{L} = \mathbf{r} \times m \mathbf{v}$$

Then

$$ \sum \mathbf{ \tau } = \dot { \mathbf{ L }} = \dot {\mathbf{ r }} \times m \mathbf{ v } + \mathbf{ r } \times m \dot { \mathbf{ v } } $$

What if the body's MOI about its own center of mass was changing? The definition doesn't seem to account for anything in the first or second term $\dot { \mathbf{r} } \times m \mathbf{v} = m r \dot r \dot \theta \mathbf{u}$ and $\mathbf{ r } \times m \dot { \mathbf{ v } } = m r \dot r \dot \theta \mathbf{u} + m r^2 \ddot \theta \mathbf{u}$

For instance: If a "wheel" with hinged spokes was expanding when given some angular velocity ( imagine a centifical clutch type mechanism ) and changing is radial distance $m r \dot r \neq \dot I$ for that case?

 

[hutchphd]

What is u ? Don't know what you are saying here.

 

[erobz]

What is u ? Don't know what you are saying here.

Its supposed to be a unit vector orthogonal to $\mathbf{r}$ and $\mathbf{v}$. I wasn't sure if we were working in polor coordinates or cylindrical coordinates, so I left it un-indexed.

 

[hutchphd]

What would $\dot I$ be for that case? Isn't $$I=mr
^2$$?

 

[erobz]

I think in that case would be:

$I = I_{\rm{CM}} + mr^2 \implies \dot I = \dot{I}_{\rm{CM}} + 2m r \dot r$

I understand this would be an unusual complexity, but I just don't want to be burned by another hidden assumption again.

 

[hutchphd]

But since $\vec{L}$ is conserved isn't its derivative always zero?

Yes that is the point. What then must happen to $\theta (t)$ ?

 

[hutchphd]

I understand this would be an unusual complexity, but I just don't want to be burned by another hidden assumption again.

Unusual? Not for the spinning skater. So why do you think this is wrong?

 

[bob012345]

Yes that is the point. What then must happen to $\theta (t)$ ?

What I meant was for the skater angular momentum is conserved so there is no derivative of angular momentum as there is in the pendulum problem.

 

[hutchphd]

The skater doesn't spin faster? The derivative exists but it is zero. Please be more careful. Perhaps a bit more thought should be applied before response.

 

[bob012345]

The skater doesn't spin faster? The derivative exists but it is zero. Please be more careful. Perhaps a bit more thought should be applied before response.

Of course the spin rate changes. I did not say it didn't. I think you misunderstood me.

 

[erobz]

Unusual? Not for the spinning skater. So why do you think this is wrong?

I think this thing would have a changing moment of inertia $I$

The terms in the torque definition from ( which I believe to be ) :

$$ \frac{d}{dt} \left( \mathbf{r} \times m \mathbf{v}\right) = \sum \tau = 2 m r \dot r \dot \theta + m r^2 \ddot \theta $$

don't seem to directly relate to $I$. None of them appear to be $\dot I$ for this system?

 

[hutchphd]

My apologies but I have lost track of what you are trying to do here. Where is r on this drawing? Have you included the parallel axis theorem in your consideration? I'm lost. Perhaps someone else understands.

 

[erobz]

My apologies but I have lost track of what you are trying to do here. Where is r on this drawing? Have you included the parallel axis theorem in your consideration? I'm lost. Perhaps someone else understands.

That last mechanism was just made up to illustrate my concern. $r$ would be the distance from the pivot to the center of the "wheel" on that drawing. And the $I$ for this system would use the parallel axis theorem, its just not clear how $I$ factors into the terms for $\tau$ above.

See, when I first was shown:

$$ L = m r^2 \dot \theta $$

the term $2 r \dot r$ came from differentiating $L$, and for a point mass the term $2 r \dot r = \dot I$, but I don't see how that is the case for the actual $I$ which might be any function.

The only thing is I would think it applies to each mass in the system individually, so in that sense the definition $\dot L = \frac{d}{dt} \left( m r^2 \dot \theta \right) \neq \frac{d}{dt}\left( I \dot \theta \right)$

I'm sorry if I am bad at explaining myself, but I am trying. It also may be the case that I have talked myself out of rationality. I'll probably wake up and see what mistake I am making. Thanks for your help.

 

[erobz]

I think this is the crux of my issue. It isn't apparent to me that the following definitions are equivalent:

$$\tau = \frac{d}{dt} \left( \mathbf{r} \times m \mathbf{v}\right) $$

$$ \tau = \frac{d}{dt} \left( I \dot \theta \right) \mathbf{u}$$

Again, $\mathbf{u}$ is just a unit vector placeholder for whatever coordinates you want to work in ( I've been scolded in PF for equating scalars and vectors previously! )

If I'm wrong, I'd like to see how?

 

[erobz]

Just to get back on track:

$(2)$ already appears to agree with the Wiki:

$$ - m \ddot r +mg \cos \theta -k\left( r - l_o \right) + mr {\dot \theta}^2 = 0 \tag{2}$$

The only thing is there is a sign difference in between the external torque terms between $(1)$ and the Wiki derivation if I take $\mathbf{r} \times m \mathbf{v} = mr^2 \dot \theta$. I'm thinking that has to come from the cross product based on my assumed convention. So $(1)$ should actually be:

$$ \sum \tau = \frac{d}{dt}\left( -m r^2 \dot \theta \right)$$

$$ rmg \sin \theta = -m \left( 2 r \dot r \dot \theta + r^2 \ddot \theta \right)$$

$$ r^2 \ddot \theta + 2 r \dot r \dot \theta + rg \sin \theta = 0 \tag{1} $$

https://en.wikipedia.org/wiki/Elastic_pendulum#Lagrangian

 

[bob012345]

I think this is the crux of my issue. It isn't apparent to me that the following definitions are equivalent:

$$\tau = \frac{d}{dt} \left( \mathbf{r} \times m \mathbf{v}\right) $$

$$ \tau = \frac{d}{dt} \left( I \dot \theta \right) \mathbf{u}$$

Again, $\mathbf{u}$ is just a unit vector placeholder for whatever coordinates you want to work in ( I've been scolded in PF for equating scalars and vectors previously! )

If I'm wrong, I'd like to see how?

I think it would be helpful to go back to fundamental definitions. Torque is defined as
$$ \large\vec{\tau} = \mathbf{r} \times \mathbf{F} $$

Expanding your first equation above
$$\large\vec{\tau} = \frac{d}{dt} \left( \mathbf{r} \times m \mathbf{v}\right) $$
$$\large\vec{\tau} = \frac{d}{dt} \left( \mathbf{r} \times \mathbf{p}\right) $$

$$\large\vec{\tau} = \frac{d}{dt} \mathbf{r} \times \mathbf{p} + \mathbf{r} \times \frac{d}{dt} \mathbf{p}$$

$$\large\vec{\tau} = \mathbf{v} \times \mathbf{p} + \mathbf{r} \times \mathbf{F}$$
but the first term is zero since $\mathbf{v}$ and $\mathbf{p}$ are parallel leaving

$$ \large\vec{\tau} = \mathbf{r} \times \mathbf{F} $$

Your second equation

$$\tau = \frac{d}{dt} \left( I \dot \theta \right) \mathbf{u}$$

is problematic if the unit vector $\mathbf{u}$ is in the direction of $\mathbf{v}$. It would be better to start with the definition of $\mathbf{L} = \mathbf{r} \times \mathbf{p}$

$$\large\vec{\tau} = \frac{d}{dt} \mathbf{L} = \frac{d}{dt} (I \mathbf{\vec{\omega}})$$

$$\large\vec{\tau} = \frac{d}{dt} \mathbf{L} = I\frac{d}{dt}\mathbf{\vec{\omega}} + \mathbf{\vec{\omega}}\frac{d}{dt}(I) $$

$$\large\vec{\tau} = \frac{d}{dt} \mathbf{L} = I\mathbf{\vec{\alpha}} + \mathbf{\vec{\omega}}\frac{d}{dt}(I ) $$
where $\mathbf{\omega}$ is a vector and $I$ a scaler.

Both ways are equivalent. The second term is not necessarily zero if $I$ changes as it does in this problem.

https://en.wikipedia.org/wiki/Torque