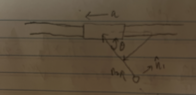
- #1
annamal
- 381
- 33
- TL;DR Summary
- I have a slider moving with a pendulum. I take the derivative of the velocity vector. Then I get the acceleration but just using a for acceleration. How come the accelerations from equations (1) and (2) [both ways of getting the acceleration] are not equal?
##\vec n_2## points to the diagonal top left.
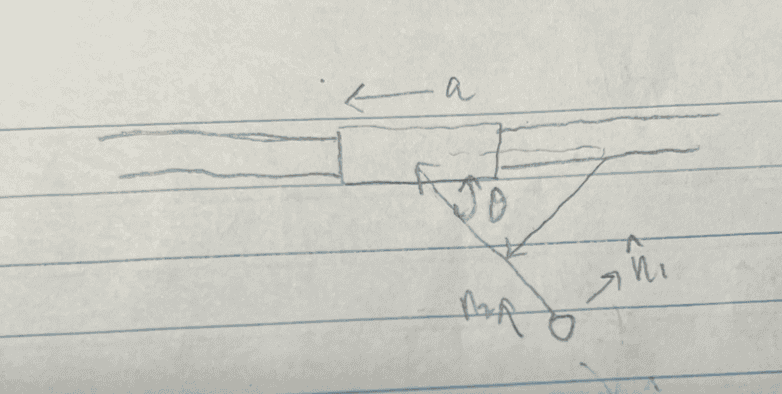
The velocity v is a function of t. So for example ##2t^2## and a = dv/dt.
Putting the velocity vector into ##\vec n_1## and ##\vec n_2## terms.
$$\vec v = v sin\theta \vec n_1 + v cos\theta \vec n_2$$
$$\vec v = -v \vec i$$
$$\vec a = \frac{d\vec v}{dt} = -a \vec i = -asin\theta \vec n_1 + acos\theta \vec n_2\ (1)$$
$$\vec a = \frac{d(v sin\theta \vec n_1 + v cos\theta \vec n_2)}{dt} = (asin\theta - 2v cos\theta \dot{\theta})\vec n_1 + (-2vsin\theta \dot{\theta} + acos\theta)\vec n_2\ (2)$$
How come ##\vec a \neq -asin\theta \vec n_1 + acos\theta \vec n_2\ (1) \neq (2)##?
The velocity v is a function of t. So for example ##2t^2## and a = dv/dt.
Putting the velocity vector into ##\vec n_1## and ##\vec n_2## terms.
$$\vec v = v sin\theta \vec n_1 + v cos\theta \vec n_2$$
$$\vec v = -v \vec i$$
$$\vec a = \frac{d\vec v}{dt} = -a \vec i = -asin\theta \vec n_1 + acos\theta \vec n_2\ (1)$$
$$\vec a = \frac{d(v sin\theta \vec n_1 + v cos\theta \vec n_2)}{dt} = (asin\theta - 2v cos\theta \dot{\theta})\vec n_1 + (-2vsin\theta \dot{\theta} + acos\theta)\vec n_2\ (2)$$
How come ##\vec a \neq -asin\theta \vec n_1 + acos\theta \vec n_2\ (1) \neq (2)##?
Attachments
Last edited: