Equation to represent the GPE of a pirate ship ride?

[minamikaze]

Homework Statement

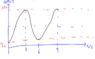
I came across the question above - and one of my peers told me that the equation E = 100(1-coskt) + a in the question is actually inaccurate in that it does not represent the motion of the pirate ship ride properly, because the equation isn't simple harmonic - the negative example to prove this was that when t = 3, kt = π radians (since k = π/3). I'm not very strong in this topic so I was unable to debate too much with him, so I wanted to get some insights from the experts here.

Homework Equations

He claims that the equation to represent the GPE of the pirate ship should be E = 100[1-cos (θ_m sin ωt)] + 30, so that the value of θ varies from 0 to 2. This would make the equation simple harmonic.

The Attempt at a Solution

I drew the graph above, and I still don't really see any problem with the GPE equation, actually. Could someone please enlighten me on this one?

Thank you so much in advance for any help!

 

[Chandra Prayaga]

I don't see anything wrong with your equation for E. It satisfies every condition laid out in the problem. So, can you now answer the questions (iii), (iv) and (v)?

 

[haruspex]

He claims that the equation to represent the GPE of the pirate ship should be E = 100[1-cos (θm sin ωt)] + 30, so that the value of θ varies from 0 to 2. This would make the equation simple harmonic.

Your fellow student is correct that the given equation is only an approximation for the motion of a pendulum that's reasonable for small swings.
In the more complicated alternative, I assume θ_m represents some unspecified function. That probably works, but does not make it SHM. (Did you mean that?) It is only SHM in the small angle approximation.

In the present problem the swing period is 12 seconds, implying a pendulum length of around 35m. For an initial height of 6m, that gives an amplitude of 34°, rather too large for the small angle approximation. So your friend's criticism is valid. Nonetheless, this is what the questioner has instructed you to use.