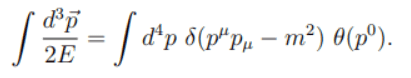SUMMARY
The discussion focuses on proving a specific equation related to Lorentz invariant quantities in the context of physics. Participants emphasize the importance of understanding the mathematical framework that underpins Lorentz invariance, particularly in special relativity. Key tools mentioned include tensor calculus and the metric tensor, which are essential for establishing the invariance of integrals under Lorentz transformations.
PREREQUISITES
- Tensor calculus
- Metric tensor in special relativity
- Understanding of Lorentz transformations
- Basic principles of special relativity
NEXT STEPS
- Study the properties of the metric tensor in Minkowski space
- Explore the derivation of Lorentz transformations
- Learn about the role of integrals in Lorentz invariance
- Investigate applications of Lorentz invariance in quantum field theory
USEFUL FOR
Physicists, students of theoretical physics, and anyone interested in the mathematical foundations of special relativity and Lorentz invariance.