dunkdie
- 1
- 0
Hi all,
I've come across this forum when searching for solution to my problem and I found that the community is extremely helpful :)
I was working on my college project when I came across the equation below.
Z = -0.0006*X^2 + 0.0004*X -0.0008*Y^2 - 0.0006*Y + 0.956
Suppose that I know the value of Z (as example Z=0.15), which method can I use to find the value of X and Y?
The equation above was derived when I was trying to chart a surface graph from these two equations:
Z = -0.0006*X^2 + 0.0004*X + 0.956
and
Z = -0.0008*Y^2 - 0.0006*Y + 0.956
However I don't know the correctness of this method that I used to come up with surface graph Z = -0.0006*X^2 + 0.0004*X -0.0008*Y^2 - 0.0006*Y + 0.956
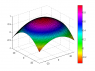
The picture of this surface graph is attached.
I tried using differential method to solve the equation but so far no luck :( Hope somebody would come up with some method or explanation regarding the matter. Many thanks.
Regards,
John
I've come across this forum when searching for solution to my problem and I found that the community is extremely helpful :)
I was working on my college project when I came across the equation below.
Homework Statement
Z = -0.0006*X^2 + 0.0004*X -0.0008*Y^2 - 0.0006*Y + 0.956
Suppose that I know the value of Z (as example Z=0.15), which method can I use to find the value of X and Y?
Homework Equations
The equation above was derived when I was trying to chart a surface graph from these two equations:
Z = -0.0006*X^2 + 0.0004*X + 0.956
and
Z = -0.0008*Y^2 - 0.0006*Y + 0.956
However I don't know the correctness of this method that I used to come up with surface graph Z = -0.0006*X^2 + 0.0004*X -0.0008*Y^2 - 0.0006*Y + 0.956
The picture of this surface graph is attached.
The Attempt at a Solution
I tried using differential method to solve the equation but so far no luck :( Hope somebody would come up with some method or explanation regarding the matter. Many thanks.
Regards,
John