Equations for Spherical Resonators

  • I
  • Thread starter DrewPear
  • Start date
  • Tags
    Spherical
In summary, the conversation discusses a web app that calculates the diameter of a sphere for a given frequency and sound hole dimensions, and allows for downloading an stl file for 3D printing. The speaker mentions issues with the equations used in the app and offers two styles based on equations from a physics professor in the 1980s. They also mention concerns about the accuracy of the equations and discuss the limitations of using only three digits in calculations. The speaker's question is whether the equations are accurate.
  • #1
DrewPear
2
2
TL;DR Summary
I'm trying to determine the accuracy of a couple of equations to determine the diameter of a sphere given the frequency and the diameter and length of a sound hole and ask related questions.
I host freely for the public a web app for determining the diameter of a sphere to resonate a given frequency and sound hole diameter and length, and then download a stl file for 3D printing. I've realized it has some issues and part of it is the equations i use to determine the sphere's diameter. I offer two styles in the app using equations given to me by a physics professor in 1980's. They are...

sphere no neck1.jpg

________________________________________________________________________________________________________________________________________

sphere with neck1.jpg
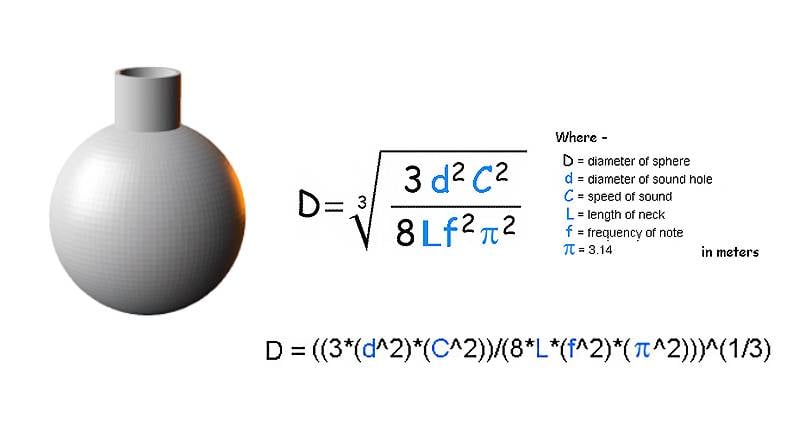At this point, i believe i should be most interested in the accuracy of the equation next to the sphere with a neck in the second picture. I've realized that the equation for a sphere with no neck in the first picture does not consider the thickness of material used since it will in essence create a neck of some length. The expression below each equation, i'm hoping, is an accurate representation of the equation above it.
 
  • Like
Likes berkeman
Physics news on Phys.org
  • #3
Baluncore said:
Welcome to PF.

Those equations are only three digits accurate, which is about the same accuracy as the temperature variation of the speed of sound.

What is your actual question ?

https://en.wikipedia.org/wiki/Helmholtz_resonance#Quantitative_explanation
https://en.wikipedia.org/wiki/Acoustic_resonance#Resonance_of_a_sphere_of_air_(vented)
Thank you.
My question is, are the equations accurate?
Do you mean three digits accurate to the right of the decimal point?
 
  • #4
DrewPear said:
Do you mean three digits accurate to the right of the decimal point?
No, I mean 3 digits in total, wherever the decimal point may be.
When Pi = 3.14 is used, there can be only three valid digits in the result.
The neck end correction has only two digits, but is inside the root computation, so all is not lost.
To get more than 3 digits, you will need to refine all constants, and correct the speed of sound in air for temperature.
 
  • Like
Likes hutchphd, Klystron and berkeman

1. What is a spherical resonator?

A spherical resonator is a three-dimensional object that can vibrate at a specific frequency when energy is applied to it. It is usually made of a solid material, such as glass or metal, and has a spherical shape.

2. How do you calculate the resonant frequency of a spherical resonator?

The resonant frequency of a spherical resonator can be calculated using the equation f = (c/2π)(n/r), where f is the resonant frequency, c is the speed of sound in the material, n is the mode number, and r is the radius of the resonator.

3. What is the relationship between the mode number and the resonant frequency of a spherical resonator?

The mode number, n, determines the number of nodes (points of zero displacement) on the surface of the spherical resonator. The resonant frequency, f, is directly proportional to the mode number, meaning that as the mode number increases, so does the resonant frequency.

4. How does the material of a spherical resonator affect its resonant frequency?

The speed of sound in a material is dependent on its density and elasticity. Therefore, different materials will have different resonant frequencies for the same size and shape of a spherical resonator. Materials with higher densities and lower elasticity will have lower resonant frequencies.

5. What are some real-life applications of equations for spherical resonators?

Equations for spherical resonators are used in various fields such as acoustics, optics, and electronics. They are used to design and analyze resonant cavities in musical instruments, lasers, and microwave filters. They are also used in the development of sensors and transducers for measuring pressure, temperature, and other physical quantities.

Similar threads

I Helmholtz resonator with multiple necks--formula?
    • Classical Physics
Replies
10
Views
4K
I Static sphere with gravitating fluid
    • Classical Physics
Replies
6
Views
297
Who Plays Saxophone? - Questions on Resonance Modes
    • Classical Physics
Replies
6
Views
1K
A Resonant frequencies of liquid in a cylinder
    • Classical Physics
Replies
14
Views
1K
Writing: Input Wanted Revisiting the Enzmann Starship Design: A Sixty-Year Perspective
    • Sci-Fi Writing and World Building
Replies
24
Views
615
How to calculate a sink using spherical coordinates
    • Calculus and Beyond Homework Help
Replies
7
Views
690
Why Is Deriving the Motion Formula for Hoops More Complex?
    • Introductory Physics Homework Help
Replies
4
Views
184
Challenge Physics Challenge: Spherical Ball Rolling on a Rough Sphere | Just for Fun!
    • Classical Physics
Replies
16
Views
2K
Deriving the Laplacian in spherical coordinates
    • Advanced Physics Homework Help
Replies
9
Views
2K
Point charge with very thin metal sheet along a spherical surface
    • Introductory Physics Homework Help
Replies
21
Views
654

Hot Threads

Recent Insights

Back
Top