hamiltoncusin
- 1
- 0
- TL;DR
- Equations of Motion for Torsional Inverted Pendulum on a moving cart using Lagrangian
Hello
I am trying to figure out the equations of motion for the following scenario: a mass m is held upright on by a massless rod mounted on a cart that is being pulled by a linear force. The caveat is that the rod is mounted on the cart via a torsional spring which causes a restorative torque as the rod swinges. Hopefully the image below can illustrate the situation
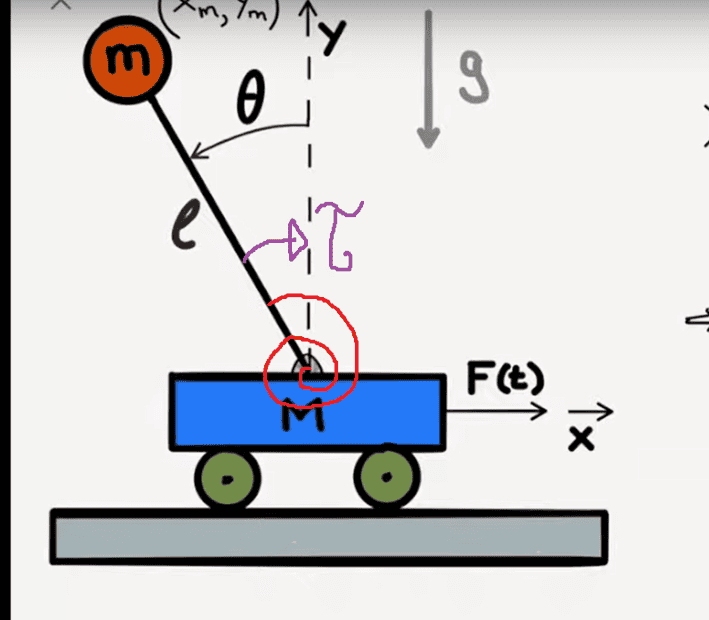
I think I figure out the equations of motion using Newton's equations and the balance of forces, however, I believe it will be easier to use Lagrangian equations. I found the video on the link below (that's where the drawing above comes from) which explains really well how to obtain the Lagrangian equations for a system without the torsional spring. My questions is then:
- I know I need to include the torsion string potential energy term in the Lagrangian, but do I need to include any generalized force related to Theta, as the video shows for x?
Here is the video:
Thanks everyone for the help
I am trying to figure out the equations of motion for the following scenario: a mass m is held upright on by a massless rod mounted on a cart that is being pulled by a linear force. The caveat is that the rod is mounted on the cart via a torsional spring which causes a restorative torque as the rod swinges. Hopefully the image below can illustrate the situation
I think I figure out the equations of motion using Newton's equations and the balance of forces, however, I believe it will be easier to use Lagrangian equations. I found the video on the link below (that's where the drawing above comes from) which explains really well how to obtain the Lagrangian equations for a system without the torsional spring. My questions is then:
- I know I need to include the torsion string potential energy term in the Lagrangian, but do I need to include any generalized force related to Theta, as the video shows for x?
Here is the video:
Thanks everyone for the help