Equilibrium angle and cable tension between collars

[RyanV]

Homework Statement

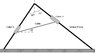
There are two collars hanging on a vertical frame made up of two smooth rods (see attached for figure). If the mass of collar A is 8 kg and the mass of collar B is 4 kg, determine the equilibrium angle \alpha and the tension in the cable between the collars.

Homework Equations

When in equilibrium, \sum F = 0

The Attempt at a Solution

The forces at Collar A,
x: T cos \alpha - Na cos 30 = 0
y: T sin \alpha + Na sin 30 - 8g = 0

The forces at Collar B,
x: -T cos \alpha + Nb sin 45 = 0
y: - T sin \alpha + Nb cos 45 - 4g = 0

where, Na and Nb are forces acting on the beams.

I've simplified the 4 equations to these two equations:

T = 4g / ( cos \alpha - sin \alpha ) ----- (1)

( sin \alpha + cos \alpha tan 30 ) = 2 ------- (2)
( cos \alpha - sin \alpha )

After that, I'm stumped. Any help?
Thanks =)

 

[pongo38]

As the rods are smooth, the reactions at the collars are perpendicular to the rods. Draw these and find their point of intersection. This should lie under the centre of mass of the collars and cable, if the sum of moments is to be satisfied.

 

[RyanV]

I'm not too sure how you would go about finding the sum of the moment at the point of intersection...Is it possible because there are no lengths given to us at all. Only angles.

I've tried it again using the reaction forces (NA/NB) of beam A and B perpendicular to the beams instead of what I did previously using the forces in the beam.

I've obtained these equations as a result:

At collar A,
x: T cos \alpha - NA sin 60 = 0
==> NA = T cos \alpha / sin 60

y: T sin \alpha + NA cos 60 - 8g = 0
==> T sin \alpha + T cos \alpha cot 60 = 8g ---- (1)


At collar B,
x: -T cos \alpha + NB cos 45 = 0
==> NB = T cos \alpha / cos 45

y: -T sin \alpha + NB sin 45 - 4g = 0
==> -T sin \alpha + cos \alpha = 4g ---- (2)


At this point, I've tried it using two different methods, but I came to a road stop each time. Maybe cause I don't have sufficient trigonometry simplification knowledge/can't see the next step/stuffed up somewhere.


Method1
(1) + (2)
T cos \alpha cot 60 + T cos \alpha = 12g
T cos \alpha ( cot 60 + 1 ) = 12g
T cos \alpha = 74.55

Need either T or \alpha to solve so came method two ...


Method2
(1)
T ( sin \alpha + cos \alpha cot 60 ) = 8g
T = 8g / ( sin \alpha + cos \alpha cot 60 )

Just looking at this equation, substituting it into the equation in method 1 would be ridiculous to solve, so I continued..hoping for something better.

(2)
- sin \alpha + cos \alpha = 4g / T
- sin \alpha + cos \alpha = ( 1/2 ) ( sin \alpha + cos \alpha cot 60 )
Further simplification gave..
( 3/2 ) sin \alpha + ( ( sqrt(3) - 6 ) / 6 ) cos \alpha = 0

I'm not sure what to do after this..


I believe this shouldn't be that ridiculously hard to solve...I probably stuffed up somewhere or unknowingly did something that you're not allowed to do..

Any help would be greatly appreciated! =D
Ryan

 

[RyanV]

No worries anymore, I've managed to solve it. =)