Valerie Prowse
- 25
- 0
Homework Statement
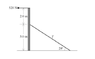
A uniform vertical beam of mass 40 kg is acted on by a horizontal force of 520 N at its top and is held, in the vertical position, by a cable as shown.
a. Draw a free-body diagram for the beam, clearly labeling all of the forces acting on it.
b. Calculate the tension in the cable
c. Determine the reaction forces acting on the beam by the ground
Homework Equations
∑Fx = 0
∑Fy = 0
∑τ = 0
The Attempt at a Solution
What I am confused about (reading other people's posts trying to work through this question) is I think I have a force missing somewhere. Some people are talking about friction force or some kind of hinge force at the bottom of the beam... I'm not sure where they are getting that information from, though. I've been reviewing problems in my textbook that are similar (they're all horizontal beams hanging from cables and hinged on a wall, though) and I can see how there could be a hinge/reaction/something force coming from the ground, but I really don't completely understand the logic behind it.
∑Fx = 0
0 = FT⋅cos28 - F
(If this were true, then you could just solve for FT, but I don't think that is correct)
If there is something missing, I feel like it would be some sort of hinge force pointing some way towards the cable, and it could be broken down into components as well... so maybe:
∑Fx = 0 = FT⋅cos28 + FH⋅cosθ - F
and
∑Fy = 0
0 = FN + FH⋅sinθ - mg - FT⋅sin28
... I'm not really entirely sure about torque yet. I'm just looking for some guidance on where to get started on this question! Thanks!