Equivalent Resistance in battery

[mbrmbrg]

Homework Statement

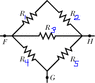
Figure 27-33 (attatched) shows five 5.00 \Omega resistors. (Hint: For each pair of points, imagine that a battery is connected across the pair.)

(a) Find the equivalent resistance between points F and H.
(b) Find the equivalent resistance between points F and G.

Homework Equations

For resistors in parallel:
R_{eq}=(\sum \frac{1}{R_i})^{-1}

For resistors in series:
R_{eq}=\Sigma R_i

The Attempt at a Solution

I solved part (a) by realizing that Resistors 1 and 2 are in series, Resistors 4 and 5 are in series, and both pairs are simultaneously in parallel with Resistor 3.
Thus:
R_{eq}=(\frac{1}{R+R}+\frac{1}{R+R}+\frac{1}{R})^{-1}
R_{eq}=(\frac{1}{10}+\frac{1}{10}+\frac{1}{5})^{-1}=2.5
So far, so good.

But for part (b), I can't come up with the correct combination. I said that Resistors 3 and 5 are in series, and they are in parallel with resistor 4. Resistors 1 and 2 are in series, but I don't see how they fit in with the rest of the circuit. I tried treating them as parallel to Resistors 3&5 and Resistor 4, and got 2.5 Ohm (wrong answer). I tried treating them as in series with Resistors 3&5 and then set all four of those resistors parallel to Resistor 4, and got 4 Ohm (still wrong).
Looking at it again, I just get more confused, because 1&2 join the circuit IN THE MIDDLE of the 3&5 series.

 

[marcusl]

The series combination R1+R2 is in parallel with R3, and that parallel combination is in series with R5. *That* series combination is in parallel with R4.

 

[mbrmbrg]

Thank you very much, that gets the right answer of 3.125 Ohm!

Do you know of a way to figure that out with as little spatial reasoning as possible? (I was the student who could do nearly everything in geometry except see the corresponding angles without turning either my head or the diagram.)

 

[xiankai]

one way is to imagine where the current is going. the shortest route from F-G is direct via R4. another path is R3+R5, which are in series and together, are parallel to R4. next, R1+R2 is parallel to R3, so we revise our calculations for R3+R5.

 

[mbrmbrg]

Hey, Zuku.

I looked at Marcusl's (wonderful!) explenation and translated it into equations.

The series combination R1+R2 is in parallel with R3, and that parallel combination is in series with R5. *That* series combination is in parallel with R4.

Must work step by step. I'm not sure how to translate this symbolically; I'll try this, and you'll tell me if it makes any sense at all.

The series combination R1+R2

R_{eq}=R_1+R_2

The series combination R1+R2 is in parallel with R3

R_{eq}=((R_1+R_2)^{-1}+R_3^{-1})^{-1}

The series combination R1+R2 is in parallel with R3, and that parallel combination is in series with R5.

R_{eq}=((R_1+R_2)^{-1}+R_3^{-1})^{-1}+R_5

The series combination R1+R2 is in parallel with R3, and that parallel combination is in series with R5. *That* series combination is in parallel with R4.

R_{eq}=((((R_1+R_2)^{-1}+R_3^{-1})^{-1}+R_5)^{-1}+R_4^{-1})^{-1}

Then shove in 5 for R, and keep very close track of the inverses, and get a numerical answer.

 

[robphy]

I solved part (a) by realizing that Resistors 1 and 2 are in series, Resistors 4 and 5 are in series,

The series combination R1+R2 is in parallel with R3, and that parallel combination is in series with R5.

I don't see that R5 is in series or in parallel with anything in this circuit... unless G is not connected to anything else but R4 and R5. The problem may have to make this explicit.

(And it's possible [especially with all of the resistors having the same value] that you get the correct numerical answer with the wrong physical reasoning.)

 

[mbrmbrg]

I don't see that R5 is in series or in parallel with anything in this circuit.

For part a:
start at point F. The current must be split through three parallel tracks in order to get to point H.

For part b:
If they don't go through R5, how else will R1, R2, and R3 be connected to point G?

 

[robphy]

For part a:
start at point F. The current must be split through three parallel tracks in order to get to point H.

For part b:
If they don't go through R5, how else will R1, R2, and R3 be connected to point G?

I see now that I think the problem is not worded well... or the picture allows some ambiguity.
I would have preferred something like:
Consider five resistors arranged as follows (without any leads running out to the edge of the image). Now ask what is the equivalent resistance between some pair of nodes [assuming nothing is connected to the remaining node]. I think the leads running to the edge of the image suggest that something else may be connected. If so, then you'd have a three-terminal device and these methods won't work. See http://en.wikipedia.org/wiki/Analysis_of_resistive_circuits