Error When Deriving the Rocket Equation

[bob14]

Homework Statement

I want to try to derive the rocket equation and then add additional effects like gravity, air resistance, etc. Here's the equation that I found online:

Homework Equations

p (momentum) = mass * velocity
F (force) = Δp / Δt

The Attempt at a Solution

[/B]

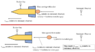
p_i = mv

Here is where the problem is. I do this:
p_final = (m - dm)(v + dv) - dm(v - v_e)

But online solutions show that it is either (m + dm) OR + dm(v - v_e), not minus.

Anyways, continuing to solve with my equation gets:
p_i = p_final (conservation of momentum)
mv = (m - dm)(v + dv) - dm(v - v_e)
mv = mv + mdv - vdm - dmdv - vdm + v_edm

Again, here the vdm should cancel, but they dont't.

mdv - dmdv = 2*vdm - v_edm

Here, I read that dmdv is considered a higher order term so it is negligible.

mdv = dm(2v - v_e)

So I got to this point but the equation is wrong. It is obvious that the mass of the rocket time dv (i.e. its change in momentum) doesn't equal the mass of the exhaust times 2v - v_e, it should just be v - v_e. But even that is wrong since it is just dm times v_e. So my question is what am I missing?

 

[TachyonLord]

p_i = p_final (conservation of momentum)
mv = (m - dm)(v + dv) - dm(v - v_e)

This is where it went wrong. You're in an inertial frame, so the momentum of the exhaust ejected is v_e)dm. I don't know why you took the relative velocity in the original equation but it will present itself in the later steps. (when you calculate the change in momentum)
∴ mv = (m - dm)(v + dv) - dm(v_e)
⇒ mv = mv + mdv - vdm - dmdv + v_edm (Im neglecting dmdv)
⇒ mdv - vdm + v_edm = 0
⇒ dm(v- v_e) = mdv

I guess you should integrate it although I can't be sure since the initial conditions aren't really mentioned.

 

[stevendaryl]

This is where it went wrong. You're in an inertial frame, so the momentum of the exhaust ejected is v_e)dm.

I think that the meaning of $v_e$ is that it is the speed of the exhaust relative to the rocket. So the velocity of the exhaust is not $v_e$ but $v - v_e$. The point is that the speed of the exhaust is not constant, but the relative velocity is (approximately).

 

[TachyonLord]

I think that the meaning of $v_e$ is that it is the speed of the exhaust relative to the rocket. So the velocity of the exhaust is not $v_e$ but $v - v_e$. The point is that the speed of the exhaust is not constant, but the relative velocity is (approximately).

Oh, I wrote my solution w.r.t. the diagram. If its the relative velocity, then momentum of the ejected mass would be dm($v + v_e$)
$v_e = v_{exhaust} - v$ Because, $v_e$ is the velocity of the ejected mass w.r.t. the rocket.
And i guess, then the cancellation takes place.

 

[bob14]

the ejected mass would be dm(v + v_e)

Ok, if I use that equation and solve, I would get:

∴ mv = (m - dm)(v + dv) + dm(v + v_e)
⇒ mv = mv + mdv - vdm - dmdv + vdm + v_edm
⇒ mdv + v_edm = 0
⇒ dm(-v_e) = mdvIntegrating would get:
-v_edm = mdv
⇒ -v_edm / m = dv
⇒ -v_e * ∫ dm / m = ∫ dv
⇒ -v_e * [ln (m_f) - ln (m₀)] = v_f - v₀ (Integrating from final to inital mass and final to initial velocity).
⇒ Δv = -v_e * ln (m_f / m₀)
⇒ Δv = v_e * ln (m₀ / m_f)

That's basically the equation that was online but I still don't get why we had to do dm(v + v_e) instead of dm(v - v_e). Doesn't the relative exhaust velocity subtract from the velocity that the rocket gave the fuel? I'm assuming that we're in the inertial reference frame of the ground, watching the rocket go up.

 

[TachyonLord]

That's basically the equation that was online but I still don't get why we had to do dm(v + v_e) instead of dm(v - v_e). Doesn't the relative exhaust velocity subtract from the velocity that the rocket gave the fuel? I'm assuming that we're in the inertial reference frame of the ground, watching the rocket go up.

Relative velocity of the mass wrt to the rocket is $v_{mass}(inertial frame) - v_{rocket}(inertial frame)$ Right ?
⇒ $v_e = v_{mass} - v$
As a result,
$v_{mass} = v_e + v$
∴ $p_{dm} = (dm)v_{mass}$
⇒ $p_{dm} = (dm)(v_e + v)$

Hope you got it ! Feel free to reply :)

 

[bob14]

Relative velocity of the mass wrt to the rocket is $v_{mass}(inertial frame) - v_{rocket}(inertial frame)$ Right ?

That part makes sense, it's just that v_mass = v_e + v doesn't. I understand its just moving the terms around but how does v_e + v work? If v_e is already negative can't we write it as v - v_e? I guess I'm looking for an intuitive way to understand it.

 

[TachyonLord]

That part makes sense, it's just that v_mass = v_e + v doesn't. I understand its just moving the terms around but how does v_e + v work? If v_e is already negative can't we write it as v - v_e? I guess I'm looking for an intuitive way to understand it.

How do you say that v_e is negative ? v_e is the velocity that I measure(of the ejected mass) if I'm sitting on the rocket, so in order to actually state if its positive/negative, you need to tell me where your origin is.

Well, It'll be ten times easier to understand if you just do it normally, I mean without bringing relative velocit into the equation first and deriving the equation with $v_{mass}$ in general.

Ill try to explain physically. Okay so like I'm already moving to the left right? Let's say that the mass is stationary(I know it isn't but let's say it is.) I'm moving with speed $v$ to the left wrt observer A. But since I'm on the rocket. I don't feel/see it. Because for me, its the mass that is moving with velocity v(or minus v whatever you want to call it).

Now, in reality the mass also has some velocity(lets say v' wrt observer A), and in fact, it is moving to the right of A. Now as the mass was stationary wrt A, I "felt" that it was already moving with velocity $v$ RELATIVE TO ME. Now when it actually starts moving with velocity $v'$, I see it moving to the right even faster, because there's an "apparent" velocity due to my movement and another velocity due to the mass itself.

As a result, it moves away faster as compared to case one. Thats why the velocities get added. Hope you get me. Again, feel free to reply !.

 

[stevendaryl]

I agree with the final equation, but I'm a little confused by the derivation, too, because of the signs.

Suppose we pick a small interval of time, $\Delta t$. Let $m_e$ be the amount of exhaust expelled during that time. Let $v_e$ be the speed of the rocket minus the speed of the exhaust. Since the exhaust is traveling backwards relative to the rocket, the rocket's speed is greater, so $v_e$ is positive.

Then conservation of momentum tells us: $m v = (m - m_e) (v + dv) + m_e (v - v_e)$. This leads to: $dv = v_e \frac{m_e}{m - m_e} \approx v_e \frac{m_e}{m}$ (since $m \gg m_e$). At this point, we use $dm = -m_e$ to get:

$dv = - v_e \frac{dm}{m} \Rightarrow v = v_0 - v_e (log(m) - log(m_0)) = v_0 + v_e (log(m_0) - log(m)) = v_0 + v_e log(\frac{m_0}{m})$

If the acceleration is from rest, $v_0 = 0$, so we get the answer.

However, in this derivation $v_e$ is the rocket's speed minus the exhaust's speed.

 

[bob14]

Now, in reality the mass also has some velocity(lets say v' wrt observer A), and in fact, it is moving to the right of A.

But with the rocket, the mass is moving to the left of A since it moves with the rocket. So wouldn't we subtract? Here's how I saw the situation (pretend I'm the stationary observer).

 

[bob14]

At this point, we use dm=−medm=−medm = -m_e to get:

Ohh, so the change in mass is negative. So that makes the v_e negative in the end. Ok, thank you so much!

 

[bob14]

Is it ok if I ask one more question?

Now that I have $Δv = v_e * ln ( \frac {m_0} {m_f})$ can I just divide by dt and multiply by m to get the force?
Like this: $m\frac {Δv} {Δt} = \frac {m * v_e * ln ( \frac {m_0} {m_f})} {Δt} = F_{thrust}$

 

[stevendaryl]

Ohh, so the change in mass is negative. So that makes the v_e negative in the end. Ok, thank you so much!

No, $v_e$ as I defined it is the rocket's speed minus the exhaust speed. Since the rocket is traveling faster than its exhaust, this is positive.

 

[bob14]

Sorry, I think I misspoke. I meant that dm is negative so the whole equation gets a negative sign in front of it.

$v_e \frac {-dm} {m}$ becomes $-v_e \frac {dm} {m}$

I didn't mean to say that v_e is negative.

 

[stevendaryl]

Is it ok if I ask one more question?

Now that I have $Δv = v_e * ln ( \frac {m_0} {m_f})$ can I just divide by dt and multiply by m to get the force?
Like this: $m\frac {Δv} {Δt} = \frac {m * v_e * ln ( \frac {m_0} {m_f})} {Δt} = F_{thrust}$

There is a little controversy over what "force" means for an object that is changing its mass. But using $F = m \frac{dv}{dt}$, you get:

$dv = - v_e \frac{dm}{m}$ so $m \frac{dv}{dt} = - v_e \frac{dm}{dt}$

 

[PeroK]

But with the rocket, the mass is moving to the left of A since it moves with the rocket. So wouldn't we subtract? Here's how I saw the situation (pretend I'm the stationary observer).
View attachment 237593

There is a trick. As acceleration is independent of inertial reference frame, you can always analyse the change in velocity of the rocket in the inertial reference frame where is it instantaneously at rest. In which case, conservation of momentum gives:

$m \Delta v = m_ev_e = -\Delta m v_e$

And this leads directly to the differential equation.

 

[bob14]

Ok thank you so much for all the help.