Edgar53
- 3
- 0
The 4-Squares-Identity of Leonhard Euler
(https://en.wikipedia.org/wiki/Euler%27s_four-square_identity) :
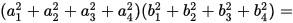
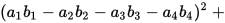
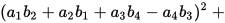
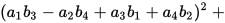
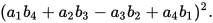
has the numeric structure of Maxwell’s equations in 4-space:
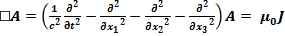
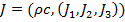
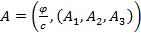
Is somebody aware of litterature about this?
(https://en.wikipedia.org/wiki/Euler%27s_four-square_identity) :
has the numeric structure of Maxwell’s equations in 4-space:
Is somebody aware of litterature about this?
Attachments
-
 upload_2017-11-19_23-4-30.jpg2.4 KB · Views: 859
upload_2017-11-19_23-4-30.jpg2.4 KB · Views: 859 -
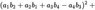 upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 886
upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 886 -
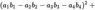 upload_2017-11-19_23-4-30.jpg1.6 KB · Views: 925
upload_2017-11-19_23-4-30.jpg1.6 KB · Views: 925 -
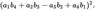 upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 411
upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 411 -
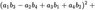 upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 483
upload_2017-11-19_23-4-30.jpg1.7 KB · Views: 483 -
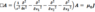 upload_2017-11-19_23-5-23.png1,018 bytes · Views: 471
upload_2017-11-19_23-5-23.png1,018 bytes · Views: 471 -
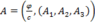 upload_2017-11-19_23-6-41.png660 bytes · Views: 456
upload_2017-11-19_23-6-41.png660 bytes · Views: 456 -
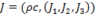 upload_2017-11-19_23-7-31.png553 bytes · Views: 448
upload_2017-11-19_23-7-31.png553 bytes · Views: 448