Euler's formula + Handshake Theorem

In summary, using Euler's formula and the Handshake Theorem, it can be shown that a graph is non-planar by checking if the values of e, v, and f satisfy certain relations. If they do not, then the graph is non-planar. Alternatively, one can also use the contradiction between the two theorems to determine the non-planarity of a graph.
  • #1
Natasha1
493
9
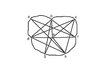
Using Euler's formula and the Handshake Theorem, how can I show that this graph is non-planar? (see graph attached)


My answer:

Euler's formula states that v+f = e+2

Here

v=8
e=21
f=?

so 8+f=21+2
hence f=15 which is not true as there are many more. Hence the graph is non-planar.

Using the Handshake Theorem that states that 2e >= 3f
we get ( 2(21) )/ 3 >= f which gives f <= 14 which again is not true, hence the graph is non-planar.

Am I correct?
 

Attachments

  • Pic 11.jpg
    Pic 11.jpg
    16.2 KB · Views: 406
Last edited:
Physics news on Phys.org
  • #2
Attatchment is still pending approval, but this is just a matter of counting right? I mean you know if it's planar e, v, and f satisfy some simple relations, therefore if they don't satisfy them it's not planar. Have some confidence!
 
  • #3
rather than using the two theorems to get results, then say that they are not true, would it not be better to use the fact that they are contradictory?
 

1. What is Euler's formula and how is it related to the Handshake Theorem?

Euler's formula, also known as the Euler characteristic, is a mathematical formula that relates the number of vertices, edges, and faces of a polyhedron. It is represented as V - E + F = 2, where V represents the number of vertices, E represents the number of edges, and F represents the number of faces. The Handshake Theorem states that in any finite undirected graph, the sum of the degrees of all vertices is equal to twice the number of edges. This theorem is closely related to Euler's formula, as it involves the same variables and can be used to solve for them in certain scenarios.

2. What is the significance of Euler's formula and the Handshake Theorem?

Euler's formula and the Handshake Theorem are important concepts in the field of mathematics, particularly in graph theory and topology. They provide a fundamental understanding of the relationship between the number of vertices, edges, and faces in a polyhedron, as well as the degrees of vertices in a graph. These concepts have various applications in fields such as computer science, engineering, and physics.

3. Can Euler's formula and the Handshake Theorem be applied to other shapes and structures?

Yes, Euler's formula and the Handshake Theorem can be applied to other shapes and structures besides polyhedrons and graphs. For example, they can be used to determine the genus or number of holes in a surface or to analyze the connectivity of a network. These concepts can also be extended to higher dimensions, such as in the study of 4-dimensional polytopes.

4. What is the proof for Euler's formula and the Handshake Theorem?

The proof for Euler's formula involves using induction and the concept of a face-edge graph. It is a fundamental result in topology and has been proven by various mathematicians, including Leonhard Euler himself. The proof for the Handshake Theorem is relatively simpler and involves using the fact that each edge in a graph is connected to exactly two vertices, and each vertex has a certain degree of connections.

5. How are Euler's formula and the Handshake Theorem used in real-world applications?

Euler's formula and the Handshake Theorem have numerous applications in real-world scenarios. In computer science, they are used in graph theory to analyze and optimize networks and algorithms. In engineering, they are used in the design and analysis of structures and circuits. In physics, they are used to understand the topology and properties of space, particularly in the study of knots and links. These concepts also have practical applications in fields such as biology, chemistry, and economics.

Similar threads

A few questions to make sure I understand Fourier series
    • Calculus and Beyond Homework Help
Replies
3
Views
264
The first and second derivatives at various points on a drawn graph
    • Calculus and Beyond Homework Help
Replies
22
Views
2K
Prove ##|\{ q\in\mathbb{Q}: q>0 \} |=|\mathbb{N}|##.
    • Calculus and Beyond Homework Help
Replies
3
Views
540
Which statements are true given a solution to the system x'=Ax?
    • Calculus and Beyond Homework Help
Replies
6
Views
1K
Determine the range of a function using parameter differentiation
    • Calculus and Beyond Homework Help
Replies
10
Views
1K
Is Tonelli's Theorem a Useful Tool for Determining the Existence of Integrals?
    • Calculus and Beyond Homework Help
Replies
10
Views
1K
Why does this proof work?
    • Calculus and Beyond Homework Help
Replies
1
Views
1K
Evaluate the Taylor series and find the error at a given point
    • Calculus and Beyond Homework Help
Replies
6
Views
2K
Determine the stability of a fixed point of oscillations
    • Calculus and Beyond Homework Help
Replies
2
Views
2K
Tricky Problem: Prove range T = null ##\phi## when null T' has dim 1
    • Calculus and Beyond Homework Help
Replies
8
Views
608

Hot Threads

Recent Insights

Back
Top