snejburg
- 3
- 0
Hey guys,
if I consider a Bernoulli-Beam with a constant jump in cross- section as shown below
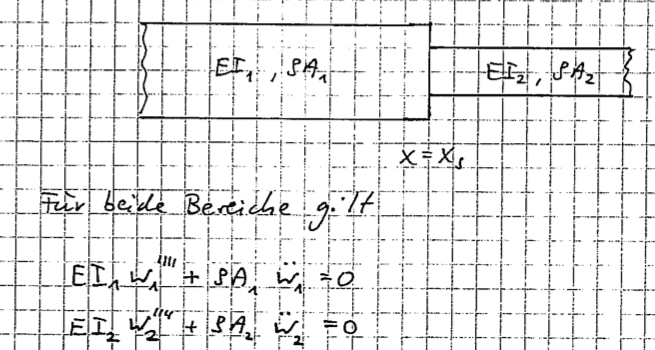
Then I get the two differential equations for the bending mentioned above.
Let us now assume that a traveling wave from the left w_incident = C*cos(k_1*x - ωt) arrives at t = 0 at the jump of cross section. If I know claim the following transition conditions:
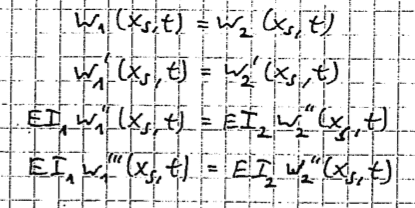
I get the following results for w_1 and w2:

The question is: How do the evanescent waves (exponential decaying waves) propagate? The formula says, that every point x of w_2 already has a displacement so that might be the steady state solution. But how can I get the transient behaviour? Therefore I need to know how the evanescent wave propagates. But I often read that evanescent waves do not propagate...But they cannot just be there all of a sudden, can they?
Your help is much appreciated,
Jens
if I consider a Bernoulli-Beam with a constant jump in cross- section as shown below
Then I get the two differential equations for the bending mentioned above.
Let us now assume that a traveling wave from the left w_incident = C*cos(k_1*x - ωt) arrives at t = 0 at the jump of cross section. If I know claim the following transition conditions:
I get the following results for w_1 and w2:
The question is: How do the evanescent waves (exponential decaying waves) propagate? The formula says, that every point x of w_2 already has a displacement so that might be the steady state solution. But how can I get the transient behaviour? Therefore I need to know how the evanescent wave propagates. But I often read that evanescent waves do not propagate...But they cannot just be there all of a sudden, can they?
Your help is much appreciated,
Jens