Evanescent Waves in near field for aperture > lambda (diffraction)?

[PhDeezNutz]

Homework Statement

This is not so much a homework question but a conceptual one. I have written a numerical program for the Vectorial Kirchhoff Integral which relates incident fields to the diffracted fields (see relevant equations). I want to treat the case of a circular aperture of radius where the aperture radius $(a\gg \lambda)$ where $lambda$ is the incident wavelength. I have created flux patterns that corroborate known formulas in both the far and near field. I have then integrated to find total flux through cubes of varying sizes (all the way from the far field to the near field) surrounding the aperture. I was hoping for power conservation and that is what I got for most part EXCEPT for in the near field I'm getting what looks like an initial evanescent wave. Is this correct? I'm finding papers that talk about initial evanescent waves in the near field for sub-wavelength apertures but not for supra-wavelength apertures (the case I am specifically treating).

Here is such a paper:

https://www.osapublishing.org/ao/abstract.cfm?uri=ao-34-17-3055

Could someone clarify if there are initial evanescent waves in the near field for supra-wavelength diffraction? (and possibly post a source)

Relevant Equations

For supra-wavelength apertures I believe the following is accurate

$\vec{E}\left(\vec{r} , z > 0 \right) = \nabla \times 2\int_{aperture} \left[\hat{z} \times \vec{E}_0 \right] \times \nabla G \left(\vec{r} , \vec{r}' \right) \,da'$


$\vec{H}\left(\vec{r} , z > 0 \right) = \nabla \times 2\int_{aperture} \left[\hat{z} \times \vec{H}_0 \right] \times \nabla G \left(\vec{r} , \vec{r}' \right) \,da'$

There are different approximation schemes to the formulas above depending on if we're in the near field or far field.

According to the textbook (Zangwill) the accepted expression for electric field in the far field is

$\vec{E} \left(r, \theta, \phi \right) = -\frac{i}{2} E_0 \left(ka \right)^2 \left( \frac{e^{ikr}}{kr}\right) \left[ \frac{2 J_1 \left(k a \sin \theta \right)}{ka \sin \theta}\right]\left(\sin \phi \hat{\theta} + \cos \phi \cos \theta \hat{\phi} \right)$

Accordingly I believe the formulas for $\vec{H}$

$\vec{H} \left(r, \theta, \phi \right) = -\frac{i}{2} H_0 \left(ka \right)^2 \left( \frac{e^{ikr}}{kr}\right) \left[ \frac{2 J_1 \left(k a \sin \theta \right)}{ka \sin \theta}\right]\left(\cos \phi \cos \theta \hat{\theta} + \sin \phi \hat{\phi} \right)$

After numerically evaluating the above integrals (in Cartesian because that is ultimately what a computer uses) I can calculate the time averaged Poynting vector numerically $\vec{S} = \frac{1}{2} \text{Re} \left( \vec{E} \times \vec{H}^*\right)$ with little difficulty.

In the near field we have (using scalar diffraction theory so this might look weird)

$E_z \left( \vec{r} \right) = \frac{E_0}{i \lambda} \int_{aperture} \frac{e^{ikr}}{r} \frac{z}{r} \, da'$

$S_z = \frac{1}{2 Z_0} \left| E_z \right|^2$

We have two different accepted formulas for the far field and near field respectively. I want a numerical program that works for both, furthermore I want to use it to calculate power through the aperture after confirming it in the far field vs near field.

I start off by treating the far field first ,where Fresnel Number $F \ll 1$, because that is what most people think of when they think about diffraction. Because the Kirchhoff Integral produces cylindrically symmetric z-flux patterns I will post cross sectional slices.

Far Field accepted formula

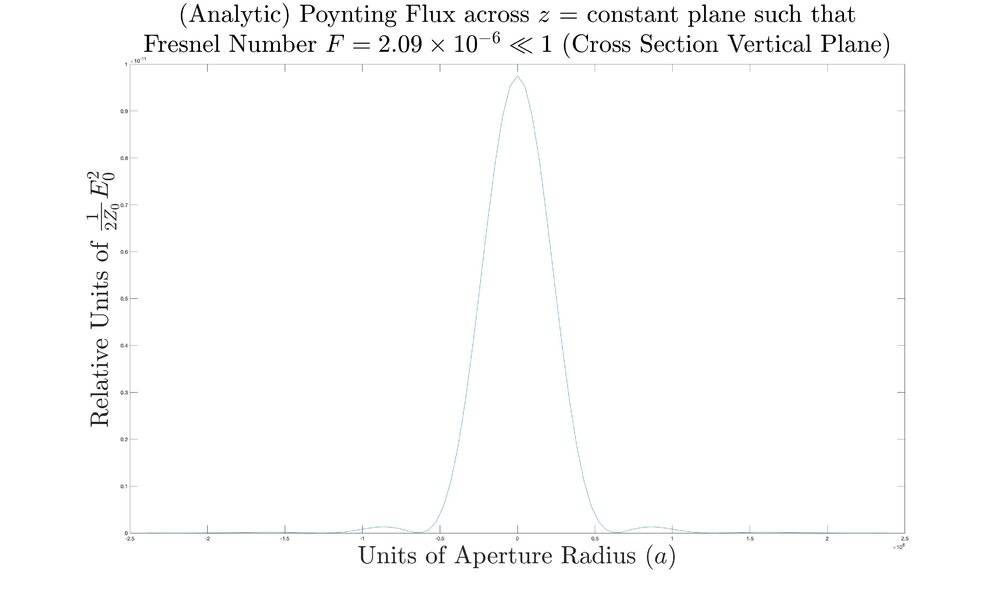
Far Field Numerical

Near Field Accepted Numerical

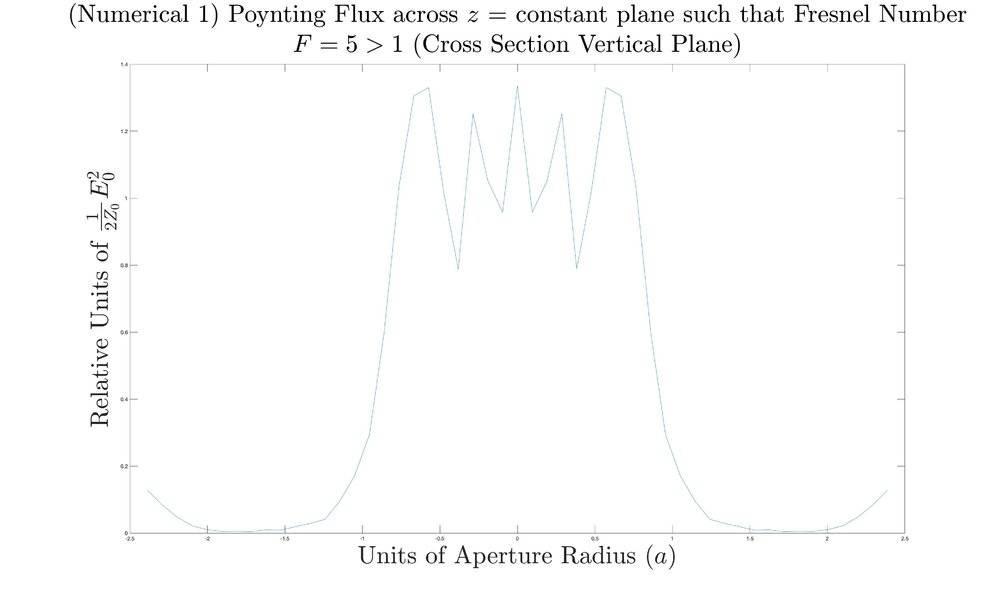
Near Field Numerical 2 (My numerical program that is supposed to be general)

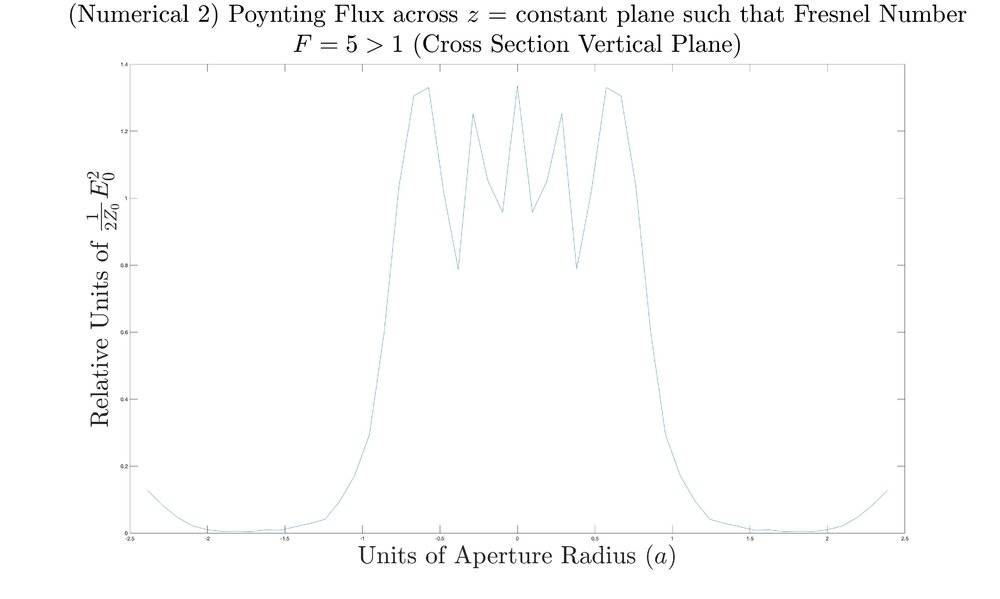
As we can see there is a strong correspondence amongst the accepted formula and my numerical formulas.Now when I graph power flux through various cubes surrounding the aperture

I get substantially up to 10% more power in the near field

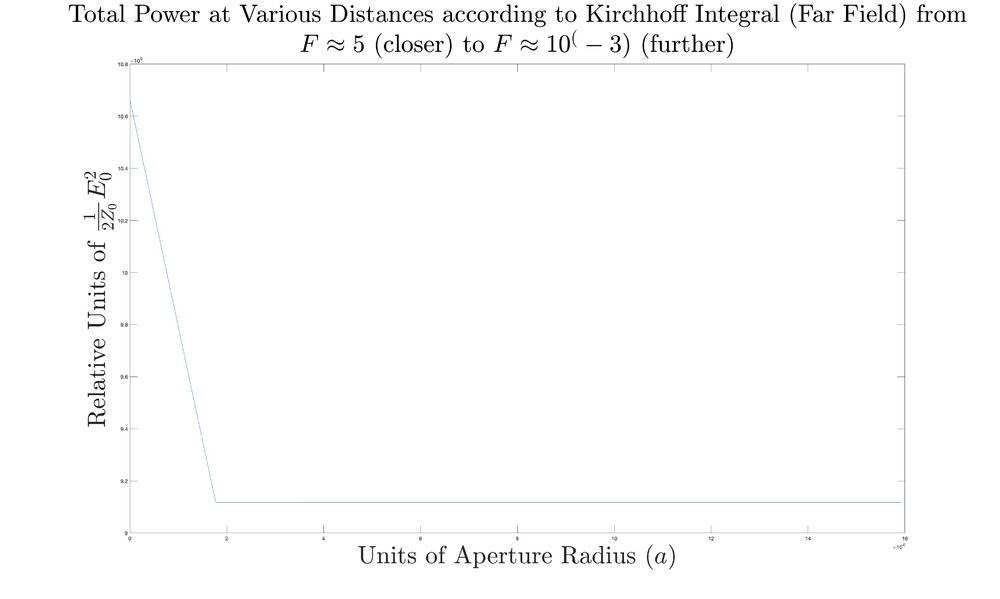
My question is:

Should this be expected in the supra-wavelength diffracting limit? I know that in the sub-wavelength diffracting limit there are initial evanescent waves

https://www.osapublishing.org/ao/abstract.cfm?uri=ao-34-17-3055

What about in the supra-wavelength diffracting limit?

Edit: My units on the vertical axis of the last graph are wrong. They should have units of Poynting Vector times area not just Poynting vector. I have to think of a good way to normalize this.

 

[Paul Colby]

To gain insight about the near field of a large circular aperture, I suggest looking at the 2D wedge or half plane scattering problem.

 

[PhDeezNutz]

To gain insight about the near field of a large circular aperture, I suggest looking at the 2D wedge or half plane scattering problem.

I think I've figured it out or at least I'm going in the right direction. Perhaps you could shed further insight. I will also look into scattering by a 2D-wedge or a half plane scattering problem.

I think it all hinges on the fact that the Kirchhoff Integral is premised on satisfying the Helmholtz Vector equation;

$\left(\nabla^2 + \frac{\omega^2}{c^2} \right) \vec{E} = 0$

The Helmholtz vector equation admits two kinds of solutions both evanescent and plane wave.

Assuming $\vec{E} = E_0 e^{-ik_x x } e^{-i k_y y} e^{-i k_z z} \hat{x}$

Then the Helmholtz characteristic equation becomes

$- k_x^2 - k_y^2 - k_z^2 + \frac{\omega^2}{c^2} = 0$

Which implies either

$k_{z1} = \sqrt{ \frac{\omega^2}{c^2} - k_y^2 - k_y^2}$ if $k_x^2 + k_y^2 < \frac{\omega^2}{c^2}$

and

$k_{z2} = i \sqrt{k_x^2 + k_y^2 - \frac{\omega^2}{c^2}}$ if $k_x^2 + k_y^2 > \frac{\omega^2}{c^2}$

I guess my question is the following. We know that any second order differential equation must have two basis functions but depending on the boundary conditions the coefficient for one of them could be zero. What diffraction boundary conditions require that we keep both types of solutions?

Said in a different way

$k_x^2 + k_y^2 < \frac{\omega^2}{c^2}$

$k_x^2 + k_y^2 > \frac{\omega^2}{c^2}$

How can both of these be satisfied simultaneously. It seems like they couldn't.

Edit: Apparently it has something to do with the completeness of the Fourier representation which is also a premise for the Vectorial Kirchhoff Integral?

 

[PhDeezNutz]

Alright I think I understand better now, can someone confirm?

The idea is to decompose the diffracted wave in the $z > 0$ half-space as a sum of plane waves. I believe this is done using a Fourier transform integrating over $k_x$ and $k_y$-space from $- \infty$ to $+ \infty$. In doing so we trace out all combinations of $k_x$ and $k_y$. If we trace out all combinations then

both

$k_x^2 + k_y^2 < \frac{\omega^2}{c^2}$

and

$k_x^2 + k_y^2 > \frac{\omega^2}{c^2}$

can be satisfied.

 

[Paul Colby]

Well, $k_z$ is determined up to a sign once the real values of $k_x$ and $k_y$ are known. For the scattered wave, real values of $k_z$, must be directed away from the aperture plane. The imaginary values of $k_z$ must be such that the fields decay as one moves further from $z=0$. This tells you how to circumvent the poles in the green function.

 

[PhDeezNutz]

I guess my question is why do we have to trace out all possible values of $k_x$ and $k_y$ and I think I know the answer now. It lies in using the "Angular Spectrum Method" where we assume the solution to the Helmholtz Equation is separable and thus its Fourier Transform\Inverse Fourier Transform is also separable. Meaning the weight function of different frequencies is separable.

1) Given field information in $z = 0$ plane; $A(x,y,z = 0)$ (assumed separable)

2) 2D-Fourier Transform (because we're decomposing it in a given plane) $A(x,y,z = 0)$

$\hat{U} \left(k_x , k_y , z = 0 \right)= \iint A\left(x,y,0 \right) e^{-ik_x x} e^{- i k_y y} \, dx dy$

(Also separable because of 1)

3) Propagate Transform to the next plane, that is merely multiply by a factor of $e^{- i k_z z}$

$\hat{U} \left(k_x , k_y , z \right) = \hat{U} \left(k_x , k_y , z = 0 \right)e^{-i k_z z}$

4) Now Inverse Fourier Transform the result from 3)

$A \left( x,y,z \right) = \frac{e^{- i k_z z}}{4 \pi^2} \iint \, \hat{U} \left(k_x , k_y , z \right) e^{i k_x x} e^{i k_y y} dk_x dk_y$

5) Why we must trace out all values of $k_x$ and $k_y$ that will either make $k_z$ real or imaginary;

The conditions

$k_{z} = \sqrt{ \frac{\omega^2}{c^2} - k_x^2 - k_y^2}$ (Propagate) if $k_x^2 + k_y^2 < \frac{\omega^2}{c^2}$

$k_{z} = i \sqrt{k_x^2 + k_y^2 - \frac{\omega^2}{c^2}}$ (Evanescent) if $k_x^2 + k_y^2 > \frac{\omega^2}{c^2}$

Trace out a circle, inside the circle we have propagation combinations and outside the circle we have evanescent combinations.

The weight function is separable$\hat{U}= U_x \left( k_x\right) U_y \left( k_y \right)$. Say we have a value of $\hat{U} \left( k_{x1} , k_{y1} \right) \neq 0$ and $\hat{U} \left( k_{x2}, k_{y2} \right) \neq 0$ just on the edge of the circle. Assuming $\left| k_{x2} \right| > \left| k_{x1}\right|$ and $\left| k_{y2} \right| > \left| k_{y1}\right|$.

$U_x \left(k_{x1}\right) \neq 0$
$U_x \left(k_{x2}\right) \neq 0$
$U_y \left(k_{y1}\right) \neq 0$
$U_y \left(k_{y2}\right) \neq 0$

If all that is true then

$U \left( k_{x1}, k_{y2} \right) \neq 0$
$U \left( k_{x2} , k_{y1} \right) \neq 0$

But since our initial points were on the circle then these new points are outside the circle. So we have non-zero weight values for evanescent modes, therefore they must be included.

I hope that makes sense. I can draw a picture if anyone wants, which of course doesn't constitute a proper mathematical proof but it is useful.

 

[Paul Colby]

Another kind of physical way to see that all k values in the plane are needed is to imagine the currents induced in modeled surface, such as a grating. Large in plane k components are required to meet the boundary conditions at the surface were high spatial frequency features are present.

 

[Paul Colby]

Also, could you use more sample points in your graphs? There seems to be a lot going on that's under sampled.

 

[PhDeezNutz]

Another kind of physical way to see that all k values in the plane are needed is to imagine the currents induced in modeled surface, such as a grating. Large in plane k components are required to meet the boundary conditions at the surface were high spatial frequency features are present.

I am not quite at that level yet but it's definitely something I will keep in mind as I learn more. Does my last "proof" seem agreeable to you? Aside from the mistakes like $U \left( k_x x, k_y y, etc\right)$ should actually be $U \left(k_x, k_y, etc \right)$ which I will edit and fix now.

Also, could you use more sample points in your graphs? There seems to be a lot going on that's under sampled.

I should do that. The problem is that each of those points was generated by brute force integration and I wanted to do it over a wide range of Fresnel Numbers without my computer taking forever to do it. In order to sample more points I will have to Isolate the near from far field.

But that's definitely something I should do and will do. I'll work on that today and post the results.

 

[Paul Colby]

without my computer taking forever to do it

I've spent a lifetime optimizing such calculations. In the end I would settle for the right answer.

 

[PhDeezNutz]

I've spent a lifetime optimizing such calculations. In the end I would settle for the right answer.

I have another more fundamental question if you don't mind.

Do we agree that

$\frac{\omega^2}{c^2} = k^2$

Then like before

$k_{z} = \sqrt{ k^2 - k_x^2 - k_y^2}$ if $k_x^2 + k_y^2 < k^2$

$k_{z} = i \sqrt{k_x^2 + k_y^2 - k^2}$ if $k_x^2 + k_y^2 > k^2$

How is the second even a possibility, I thought the definition of $k$ is literally

$k = \sqrt{k_x ^2 + k_y ^2 + k_z^2}$

wouldn't $k_x^2 + k_y^2 > k^2$ violate the so-called "triangle inequality"

I still plan on posting graphs with more points.EDIT: I think I got it now, can someone confirm?

$\frac{\omega}{c^2} \neq k^2$ ( I guess you can call it $k^2$ but you have to be mindful of what it means)

$\omega$ is the time frequency where as $k_x$,$k_y$,and $k_z$ are the independent spatial frequencies. The notion of characterizing a 3D wave by a single overall spatial frequency is meaningless because we have 3 directions that are independent;

$k = \sqrt{k_x^2 + k_y^2 + k_z^2}$ is a meaningless statement because what would that even represent? $k_{x,y,z}$ represents the number of waves that pass a point in the $x,y,z$ directions respectively. $k = \sqrt{k_x^2 + k_y^2 + k_z^2}$ wouldn't represent the number of waves passing an arbitrary point...That would be represented by $\vec{k} \cdot \vec{r}$. Long and short of it; I think $k$ without subscripts is a meaningless notion in 3D.

EDIT: Another question: Can evanescent waves excite modes in a waveguide or resonant cavity?

 

[Paul Colby]

I have another more fundamental question if you don't mind.

Do we agree that

$\frac{\omega^2}{c^2} = k^2$

Then like before

$k_{z} = \sqrt{ k^2 - k_x^2 - k_y^2}$ if $k_x^2 + k_y^2 < k^2$

$k_{z} = i \sqrt{k_x^2 + k_y^2 - k^2}$ if $k_x^2 + k_y^2 > k^2$

How is the second even a possibility, I thought the definition of $k$ is literally

yes, the characteristic equation (the first equation) is correct. If you substitute the third equation into the first you’ll see this is the case. Of course you’ll need to replace $k^2$ with $\omega^2/c^2$ to see this.

Also, keep in mind that every square root has 2 possible values. You must choose which of these values are the physical ones. This is where the far field boundary conditions are met.

 

[Paul Colby]

I think I got it now, can someone confirm?

$\omega^2/c^2\ne k^2$ ( I guess you can call it $k^2$ but you have to be mindful of what it means)

No, this is not correct.

 

[Paul Colby]

So, let’s try this on for size. You can write the fields above the plane as a sum over all possible plane wave solutions because the equations are linear. All possible plane waves includes all possible complex vectors, $k$, which obey,

$k\cdot k = \frac{\omega^2}{c^2}$

where the right hand side is real and fixed. Now, look at any of these vectors with a complex, $k_x$. You can see that these can be thrown out because they become infinite at either plus infinity in x or minus infinity in x. So, $k_x$ real are the only suitable choices. Same goes for $k_y$. Now, for $k_z$ things are different. Some Complex values are permitted if they don’t blow up at infinity. Repeat for an expression below the plane.

 

[PhDeezNutz]

yes, the characteristic equation (the first equation) is correct. If you substitute the third equation into the first you’ll see this is the case. Of course you’ll need to replace $k^2$ with $\omega^2/c^2$ to see this.

Also, keep in mind that every square root has 2 possible values. You must choose which of these values are the physical ones. This is where the far field boundary conditions are met.

No, this is not correct.

I think I get it now, I was restricting $k_x$ and $k_y$ to be real and that's why the statements

$k^2 = k_x^2 + k_y^2 + k_z^2$ and $k_x^2 + k_y^2 > k^2$ didn't make sense to me. If we allow $k_x$ and $k_y$ to be complex/imaginary then we can get negative values for $k_x^2$ and $k_y^2$ which allows $k_x^2 + k_y^2 > k^2$ to be true.

Edit: you beat me to it. NVM it seems like your post directly above is different. I'll read it again.

 

[PhDeezNutz]

Why do we have to throw out imaginary $k_x$ if we're only concerned about the half-space $z > 0$?

if $k_x$ is imaginary and proportional to $-i$ in the half space $z>0$ then $e^{-ik_x x}$ would correspond to an evanescent wave wouldn't it? Because it would take on the form $e^{-cx}$ in the half space $z>0$.

 

[Paul Colby]

Why do we have to throw out imaginary $k_x$ if we're only concerned about the half-space $z > 0$?

if $k_x$ is imaginary and proportional to $-i$ in the half space $z>0$ then $e^{-ik_x x}$ would correspond to an evanescent wave wouldn't it? Because it would take on the form $e^{-cx}$ in the half space $z>0$.

Well, a solution going like $e^x$ isn’t acceptable physically. A solution going like $e^{-x}$ is no better.

 

[PhDeezNutz]

Well, a solution going like $e^x$ isn’t acceptable physically. A solution going like $e^{-x}$ is no better.

Isn't $e^{-x}$ in the half-space $z>0$ (where the diffraction pattern is observed) valid because it goes to 0 in the long run? These are my initial thoughts, I will take a closer look at your post #14 and report back.

 

[PhDeezNutz]

@Paul Colby I'm an idiot. In the $z>0$ half space we have both positive and negative $x$. Same goes for $y$. Your post 14 makes perfect sense now.

 

[Paul Colby]

Isn't $e^{-x}$ in the half-space $z>0$ (where the diffraction pattern is observed) valid because it goes to 0 in the long run? These are my initial thoughts, I will take a closer look at your post #14 and report back.

The plane includes both +x and - x. Infinity in either direction aren’t allowed because infinite energy density in either direction is unphysical. This holds on both sides of the plane.

 

[Paul Colby]

Just a simple fact or aside that I find helpful to keep in mind. A complex 3 vector, $k$, may be written as a real and imaginary vectors, or

$k = A + iB$

where, A and B are just real three vectors. Now what if, $k\cdot k=R^2$, where R is real? Well,

$k\cdot k = (A\cdot A - B \cdot B) + 2i(A\cdot B)$

so that,

$R^2 = A\cdot A - B\cdot B$

and

$A\cdot B = 0$.

I think this helps understand the interplay of the real and complex components more clearly.

 

[PhDeezNutz]

@Paul Colby

I think I've constructed a better mathematical argument for the inclusion of ALL modes (Evanescent and Propagating) that doesn't hinge on separability.

It requires me to re-cap and re-formulate the "Angular Spectrum Method" and then do my "proof". The gist of it is that if the weight function for frequencies $\hat{U} \left(k_{x1},k_{y1},z\right) = 0$ for a certain $k_{x1}$ and $k_{y1}$ then $\hat{U} \left( k_{x1}, k_{y1}, z = 0\right) = 0$. If $\hat{U} \left( k_{x1}, k_{y1}, z = 0\right) = 0$ then $U \left( x , y, z = 0\right) \equiv 0$ at which point we don't even have a problem to consider.

Let me recap the Angular Spectrum Method

Step 0) $U(x,y,z)$ (intensity) is a manifestly positive quantity.

Step 1) Given intensity in the $z=0$ plane: $U\left( x, y, z = 0\right)$ we Fourier Transform to $k\text{-space}$

$\hat{U} \left( x, y, z \right) = \int_{-\infty}^{+\infty} U \left(x,y,z= 0 \right) e^{-ik_x}E^{-ik_y y}\,dx dy$

Step 2) We propagate $\hat{U}\left( k_x,k_y, z = 0\right)$ to the next $z\text{-plane}$ by means of multiplying by $e^{-i k_z z}$

$\hat{U} \left(k_x, k_y, z \right) = \hat{U} \left(k_x, k_y, z = 0 \right)e^{i k_z z}$

Step 3) We take the inverse Fourier Transform of $\hat{U} \left(k_x, k_y, z \right)$ to get the resulting intensity in position space

$U\left(x,y,z\right) = \frac{1}{4 \pi^2} \int_{-\infty}^{\infty} \hat{U} \left( k_x, k_y, z\right) e^{ik_x x}e^{i k_y y} \, dk_x dk_y$

Now for the proof that if any of the modes (evanescent or propagating) are excluded then $U\left(x,y,z= 0\right) \equiv 0$ which of course means we have a trivial non-existent problem.

1) Suppose $\hat{U} \left( k_{x1}, k_{y1}, z \right) = 0$ for a certain $\left( k_{x1},k_{y1},z\right)$

2) That would imply according to Step 2 that $\hat{U} \left(k_{x1}, k_{y1}, z = 0 \right) = 0$ because oscillatory terms cannot be equal to 0

3) If $\hat{U} \left(k_{x1}, k_{y1}, z = 0 \right) = 0 \Rightarrow U \left( x,y, z = 0\right) \equiv 0$ for all $\left(x,y\right)$ since we're integrating a manifestly non-negative quantity (intensity) over all space and oscillatory terms cannot equal $0$.

4) If $U \left( x,y, z = 0\right) \equiv 0$ then that would mean we don't even have a problem to consider according to Step 1; If the intensity is identically $0$ in one plane then it will be identically $0$ in another plane.

 

[Paul Colby]

Where does your proof use the field equations? Clearly, $$k_z(k_x,k_y)=\pm\sqrt{k^2-k_x^2-k_y^2},$$ right? What demands all real $k_x$ and $k_y$ is meeting the boundary conditions on the plane $z=0$. You can see this by considering the no aperture limit. In this case only 2 real k plane waves are required to meet the boundary connections.

 

[PhDeezNutz]

Forgot to mention that at the beginning. I assumed $k_x$ and $k_y$ were real for the very reasons you mentioned (solutions have to converge) and then argued that we must consider all values of real $k_x$ and $k_y$ because if the weight function for frequencies for a certain $k_{x1}$ or $k_{y1}$ were equal to zero that would imply the initial intensity would have to be zero (at which point we don't even have a problem to consider).

Suppose $\hat{U}\left( k_{x1}, k_{y1}, z \right) = 0$

That would imply $\hat{U} \left( k_{x1}, k_{y1}, z = 0 \right) = 0$ since

$\hat{U}\left( k_{x1}, k_{y1}, z \right) = \hat{U} \left( k_{x1}, k_{y1}, z = 0 \right) e^{-ik_z z}$

As we know an oscillatory term cannot equal 0 so the non-oscillatory term has to be equal to 0.

If we have $\hat{U} \left( k_{x1}, k_{y1}, z = 0 \right) = 0$ then we also have

$0 = \int_{-\infty}^{+\infty} U \left(x,y,z=0\right) e^{-i k_x x} e^{-i k_y y} \, dk_x dk_y$ by Step 1) (which I wrote wrong before) which says

$\hat{U} \left( k_{x1}, k_{y1}, z = 0\right) = 0 = \int_{-\infty}^{+\infty} U\left(x,y,z=0\right)e^{-i k_{x1} x} e^{-i k_{y1} y} \, dx dy$

The only way to integrate a manifestly non-negative quantity over all space to get 0 is if the integrand is 0 for all values of $x$ and $y$ Oscillatory terms cannot equal 0 so that would imply $U \left( x, y,z = 0\right) \equiv 0$

But if $U \left( x, y,z = 0 \right) \equiv 0$ then we don't even have a problem to consider.

Which is why $\hat{U}\left( k_{x1}, k_{y1}, z \right) \neq 0$ for any combination of real $k_{x1}$ and $k_{y1}$.

 

[Paul Colby]

Sorry, I don't see the point of this proof which seems to be $0=0$ using Fourier transforms. How does this help you?

 

[PhDeezNutz]

Sorry, I don't see the point of this proof which seems to be $0=0$ using Fourier transforms. How does this help you?

I was trying to prove that all real $k_x, k_y$must be accounted for and that the weight function value for any real $k_x, k_y$ never takes on the value of 0. Thus they must be included and thus we have evanescent modes.It could be very well that I'm barking up the wrong tree/being pedantic, I have been known to hyper-focus and miss the point. Or it could be that I have a point and I'm just bad at expressing it. I'll try to clarify.

It's sort of a proof by contradiction; if $\hat{U} \left( k_x, k_y, z \right) = 0$ for any possible real $k_x$ and $k_y$ then $U\left(x,y,z = 0\right) \equiv 0$ for all $\left(x,y, z = 0\right)$ which is a trivial problem when propagated gives us zero for all $(z > 0)$ half-space. But we know before hand (experimentally) that the diffraction pattern is NOT $0$ for all of the $(x,y,z>0)$ so $\hat{U} \left( k_x, k_y, z \right) \neq 0$ for any real $k_x, k_y$. That is to say the weight function value for all combinations of real $k_x, k_y$ never takes on the value of $0$.

 

[Paul Colby]

I was trying to prove that all real kx,kymust be accounted for and that the weight function value for any real kx,ky is never takes on the value of 0. Thus they must be included and thus we have evanescent modes.

Yes, but that's actually false. Look at a conducting plane with no aperture. The solution is the incident plane wave, $$\mathbf{k}_i = k(\sin\theta,0,\cos\theta),$$ where, $\theta$, is the angle of incidence. The reflected wave is $$\mathbf{k}_r = k(\sin\theta,0,-\cos\theta).$$ So the weight function is zero almost everywhere.

 

[Paul Colby]

Again, the only reason the evanescent waves are required is to meet the boundary conditions on the plane. It's like fitting a square pulse. All wavelengths are needed to make this happen.

 

[Paul Colby]

Another case to consider is an infinite slot in the plane. If the slot is along x, no evanescent waves are needed or present in x.

 

[PhDeezNutz]

Again, the only reason the evanescent waves are required is to meet the boundary conditions on the plane. It's like fitting a square pulse. All wavelengths are needed to make this happen.

I think I see your reasoning. The wave doesn't just go through the aperture and spread out in the forward direction. In addition it spreads out over the rest of the conducting surface in the forward half space.

1) As we know frequencies must be continuous across boundaries for energy conservation

2) we also know that waves decay exponentially inside a good conductor (evanescent)

If 2 is true then according to 1 we must have evanescent waves just outside the conductor.

Am I on the right track?

Also thank you for being patient with me. I really appreciate all your help.

 

[Paul Colby]

No, I don't think #30 is the right track. One can assume a perfect conductor and an infinitely thin plane. Look at the tangent electric field. It's zero everywhere in the plane except inside the aperture. Inside the aperture it's not zero. One only needs to compute for this tangent field since the field everywhere else may be computed with a radiation integral involving a green function. One does this by treating the tangent electric field crossed with the plane normal as a magnetic current.

So, what one should be doing is computing the aperture field which means solving the boundary value problem. I really suggest you view this as adding together plane wave solutions such that the boundary conditions are met. Do you know what these conditions are?

 

[Paul Colby]

It occurs to me there may be a simple approach solution to the scattering of a plane wave from an aperture which would use what you've been posting on.

The first step is to start with a solvable problem, the infinite conducting plane reflecting a plane wave. The solution is $$ E(r)= E_i e^{-ik_i\cdot r} + E_r e^{-ik_r\cdot r},\text{ (1)} $$ where the constant polarization vector $E_r$ is chosen so that the total tangent field is zero on the plane $z=0$. Now, we drill a hole in our screen. Two things happen inside the hole. The first is there is now a tangent E-field. The second is there is no longer a surface current induced by the incident and reflected waves. Before we cut the hole the surface current from (1) is, $$J=\hat{z}\times\nabla\times E,\text{ (2)}$$The solution of the problem is obtained by adding a solution to the field equations which removes the surface current, $J(x,y)$, just within the hole. If one expands, $J(x,y)$, in terms of a Fourier series (like you've been doing) and adds in the z-dependence (as you've been doing) one gets just this field and the solution to the problem. Lot's of messy details left out here like sign choices for $k_z(k_x,k_y)$ but I'll leave that to you.

 

[PhDeezNutz]

It occurs to me there may be a simple approach solution to the scattering of a plane wave from an aperture which would use what you've been posting on.

The first step is to start with a solvable problem, the infinite conducting plane reflecting a plane wave. The solution is $$ E(r)= E_i e^{-ik_i\cdot r} + E_r e^{-ik_r\cdot r},\text{ (1)} $$ where the constant polarization vector $E_r$ is chosen so that the total tangent field is zero on the plane $z=0$. Now, we drill a hole in our screen. Two things happen inside the hole. The first is there is now a tangent E-field. The second is there is no longer a surface current induced by the incident and reflected waves. Before we cut the hole the surface current from (1) is, $$J=\hat{z}\times\nabla\times E,\text{ (2)}$$The solution of the problem is obtained by adding a solution to the field equations which removes the surface current, $J(x,y)$, just within the hole. If one expands, $J(x,y)$, in terms of a Fourier series (like you've been doing) and adds in the z-dependence (as you've been doing) one gets just this field and the solution to the problem. Lot's of messy details left out here like sign choices for $k_z(k_x,k_y)$ but I'll leave that to you.

That sound promising but difficult. But also enlightening and worthwhile. I will work on it for the remainder of the day and hopefully get something that’s respectable enough to work with.

I really can’t thank you enough for all your help.

 

[PhDeezNutz]

Again, the only reason the evanescent waves are required is to meet the boundary conditions on the plane. It's like fitting a square pulse. All wavelengths are needed to make this happen.

I think I understand this. The aperture function (or field in the aperture) is literally a square pulse (say for a single slit aperture) and therefore you need all frequencies to construct it.

$\hat{U} \left(k_x , k_y , z = 0 \right)= \iint A\left(x,y,0 \right) e^{-ik_x x} e^{- i k_y y} \, dx dy$

In the usual Kirchhoff Integral style we assume the field in the aperture is the same as the incident field (which is probably not true but it works).

So

$A\left(x,y,0\right)$ =

$0$ if $x \lt -a$

$A_0$ if $-a \leq x \leq a$

$0$ if $x \gt a$

​

If we take the Fourier transform of this aperture function (which is essentially a square wave) we get all frequencies. Is this what you meant?

 

[Paul Colby]

Yes. I might add that for some range of aperture size, assuming the aperture field is just the incident field i expect would give a reasonable approximation for the radiation pattern. In fact this approximation is useful in designing waveguide antennas.