Cross section from subgraph in electron-proton DIS

[weningth]

I am currently following R.K. Ellis et al.: QCD and Collider Physics, pp. 99 to understand how to arrive at the parton density functions starting from the matrix elements in electron-proton deep inelastic scattering (see figure below). But there seems to be a very fundamental concept that I don't understand at all.

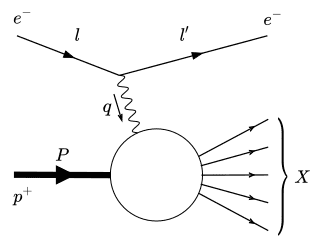
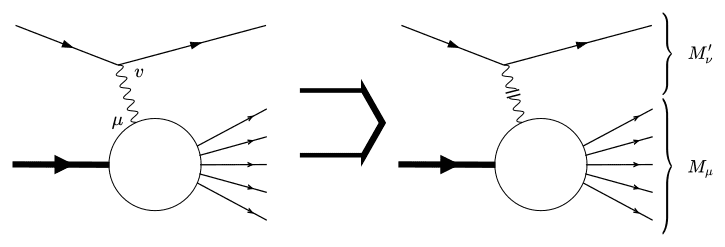
In the book mentioned above, the matrix element is split up into a leptonic part $M_\nu$ and a hadronic part $M^\prime_\mu$ connected by the photon propagator (see figure below). From the hadronic part (without the photon propagator attached) they then calculate a matrix element, square it, average over spin, polarisations and colours and then calculate a differential cross section from it.

There are several points, which confuse me about this.

• Matrix elements have external states attached to it. Here, however the leptonic part with its spinors is missing. How is it possible to define a physically meaningful S-matrix element from the hadronic part only?
• How do the differential cross section of the entire Feynman graph and of the hadronic subgraph relate to each other?
• How can I justify throwing out the entire leptonic subgraph from all my calculations, even when squaring the matrix element? After all $|M|^2=|M_\nu\frac{-ig^{\mu\nu}}{q^2}M^\prime_\mu|^2\neq|M_\nu\frac{-ig^{\mu\nu}}{q^2}|^2\times|M^\prime_\mu|^2$.

 

[Reggid]

The leptonic part is not thrown out, and the amplitude is not squared in the way you write it out here.

You look at the process $e+P\to e+X$. Let's denote the momentum of the electron before and after the scattering by $k$ and $k^\prime$, the proton momentum by $P$ and the momentum of the hadronic final state as $P_X$, and define the invariants
Q^2=-q^2
x_B=\frac{-q^2}{2P\cdot q}
s=(P+k)^2
with $q=k-k^\prime$.

Then the differential cross section is
\frac{\mathrm{d}\sigma}{\mathrm{d}x_B\mathrm{d}Q^2}=\frac{1}{(4\pi)^2}\frac{Q^2}{s^2x_B^2}\sum_X\mathrm{d}\Pi_X(2\pi)^4\delta^{(4)}(P+q-P_X)|\mathcal{M}|^2

The amplitude $\mathcal{M}$ to leading order in QED is
\mathcal{M}(eP\to eX)=\bar{u}(k^\prime)(-ie\gamma_\mu)\frac{-i}{q^2}(ie)\langle X|J^{\mu}(0)|P\rangle
with the electromagnetic current of the quark fields $q_i$ of all possible flavors $i$ with charge quantum number $\mathcal{Q}_i$
J^{\mu}(x)=\sum_i\mathcal{Q}_i\bar{q}_i(x)\gamma^{\mu}q_i(x)
Then the spin-averaged square of the amplitude is
|\mathcal{M}|^2_{\rm{spin-av.}}=\frac{32\pi^2\alpha^2}{Q^4}L_{\mu\nu}\langle P|J^{\mu}(0)|X\rangle\langle X|J^{\nu}(0)|P\rangle
where the leptonic tensor is defined as
L_{\mu\nu}=k_\mu k^\prime_{\nu}+k_{\nu}k^{\prime}_{\mu}-k\cdot k^{\prime}g_{\mu\nu}
You see that the leptonic side is of course not thrown away.

When you define the hadronic tensor $W^{\mu\nu}$ as
W^{\mu\nu}=\frac{1}{4\pi}\sum_X\mathrm{d}\Pi_X(2\pi)^4\delta^{(4)}(P+q-P_X)\langle P|J^{\mu}(0)|X\rangle\langle X|J^{\nu}(0)|P\rangle
then the cross section can be written in the simple form
\frac{\mathrm{d}\sigma}{\mathrm{d}x_B\mathrm{d}Q^2}=\frac{4\pi\alpha^2}{Q^2s^2x_B^2}L_{\mu\nu}W^{\mu\nu}

The hadronic tensor can be also written in the form
W^{\mu\nu}=\frac{1}{4\pi}\int\mathrm{d}^4x\mathrm{e}^{ixq}\langle P|J^{\mu}(x)J^{\nu}(0)|P\rangle
(which is equivalent to the definition above) and that is the object for which you can then calculate QCD corrections and which you can factorized into the PDF and the hard Wilson coefficient.

 

[weningth]

Do you have any reference where it is explicitly shown how to acquire that specific form of the cross section and the equivalence of the two definitions of the hadronic tensor? As for the matrix element, I find the exact same result.

 

[Reggid]

Well, for the cross section you just start from the normal $1+2\to 3+4+...$ cross section that you find in every textbook, and just separate the phase space integration of the outgoing electron with momentum $\vec{k}^\prime$ from the hadronic final state particles (and set the masses of the proton and the electron to zero).
\mathrm{d}\sigma=\frac{1}{2s}\frac{\mathrm{d}^3k^\prime}{(2\pi)^3}\frac{1}{2|\vec{k}^\prime|}\sum_X\mathrm{d}\Pi_X(2\pi)^4\delta^{(4)}(P+q-P_X)|\mathcal{M}|^2
Then you can derive the relation
\frac{\mathrm{d}^3k^\prime}{(2\pi)^3}\frac{1}{2|\vec{k}^\prime|}=\frac{\mathrm{d}x_B\mathrm{d}Q^2}{(4\pi)^2}\frac{Q^2}{x_B^2s}
and arrive at the cross section given in my first post.

For the hadronic tensor you can use
(2\pi)^4\delta^{(4)}(P+q-P_X)=\int\mathrm{d}^4x\,\mathrm{e}^{i(P+q-P_X)x}
the fact that $|X\rangle$ and $|P\rangle$ are eigenstates of the momentum operator $\hat{P}$, the fact that the momentum operator is the generator of spatial translation, i.e.
\mathrm{e}^{i\hat{P}x}J^{\mu}(0)\mathrm{e}^{-i\hat{P}x}=J^{\mu}(x)
and the completeness relation
\sum_X\mathrm{d}\Pi_X\,|X\rangle\langle X|=\mathbf{1}