Expanding (i) and Solving (ii): Find the Solution

[chwala]

Homework Statement

See attached problem with ms

Relevant Equations

binomial theorem

Find question here and ms... In part $i$ we could just as well expand directly hence reason why i am sharing...

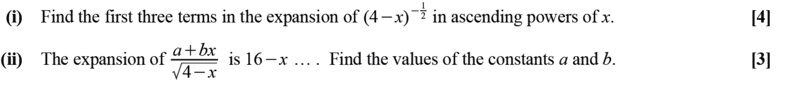
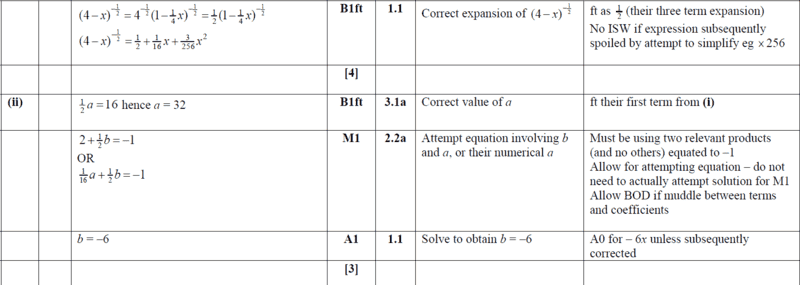
My direct expansion for part (i),

$$(4-x)^{-\frac{1}{2}} =4^{-\frac{1}{2}}+\frac{(\frac{-1}{2}⋅4^{-\frac{3}{2}}⋅-x)}{1!}+\frac {(\frac{3}{2}⋅\frac{1}{2}⋅4^-\frac{5}{2}⋅(-x)^2)}{2!}=\frac{1}{2}+\frac{1}{16}x+\frac{3}{256}x^2+...$$

part (ii) follows directly from (i),

$(a+bx)(\frac{1}{2}+\frac{1}{16}x+\frac{3}{256}x^2+...)=16-x...$
$\frac{1}{2}a+\frac{1}{16}ax+\frac{3}{256}ax^2+\frac{1}{2}bx+\frac{1}{16}bx^2+\frac{3}{256}bx^3+...=16-x...$

giving us the two simultaneous equations indicated. cheers

 

[anuttarasammyak]

As an alternative way
$$(\frac{a+bx}{\sqrt{4-x}})_{x=0}=\frac{a}{2}=16$$
a=32
$$(\frac{32+bx}{\sqrt{4-x}})'_{x=0}=\frac{b+4}{2}=-1$$
b=-6

 

[chwala]

As an alternative way
$$(\frac{a+bx}{\sqrt{4-x}})_{x=0}=\frac{a}{2}=16$$
a=32
$$(\frac{32+bx}{\sqrt{4-x}})'_{x=0}=\frac{b+4}{2}=-1$$
b=-6

Smart move there @anuttarasammyak ...just wondering if this approach would be acceptable, i.e substituting $x=0$ directly ... are we not supposed to make use of part (i) though?

I can see that its a B mark, thus acceptable...cheers