dobry_den
- 113
- 0
Hi! I came over this paradox: an Erlenmeyer flask and a beaker are filled with water to the same height - it is assumed that they have the same base area and the same mass. Then the hydrostatic pressure of water is the same at the bottom of each container (since the depths are the same) and when put on a balance, they should exert the same force on it and therefore weigh the same. The question is - what's wrong?
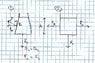
I think it might be that one should take into account all the forces acting on the containers. In the case of the beaker, there's the force that's acts on the base plus forces that act on the sides of the beaker. The forces acting on the sides should cancel themselves - when we look at every vertical cut of the beaker that goes through its axis, the forces on opposite sides are equal in magnitude (due to the Pascal's Law - "the fluid pressure at all points in a connected body of an incompressible fluid at rest, which are at the same absolute height, are the same") and opposite in directions.
In the case of the flask, these forces are perpendicular to its sides. Horizontal components cancel out. But for the paradox stated above, their vertical components are important, since they are responsible for reducing the force acting on the balance - they reduce the effect of the hydrostatic force acting on the base of the flask.
I also attached a drawing. Is this a good answer to the initial question "What's wrong (in the case of the flask)?"
I think it might be that one should take into account all the forces acting on the containers. In the case of the beaker, there's the force that's acts on the base plus forces that act on the sides of the beaker. The forces acting on the sides should cancel themselves - when we look at every vertical cut of the beaker that goes through its axis, the forces on opposite sides are equal in magnitude (due to the Pascal's Law - "the fluid pressure at all points in a connected body of an incompressible fluid at rest, which are at the same absolute height, are the same") and opposite in directions.
In the case of the flask, these forces are perpendicular to its sides. Horizontal components cancel out. But for the paradox stated above, their vertical components are important, since they are responsible for reducing the force acting on the balance - they reduce the effect of the hydrostatic force acting on the base of the flask.
I also attached a drawing. Is this a good answer to the initial question "What's wrong (in the case of the flask)?"