- #1
Ravi Singh choudhary
- 125
- 7
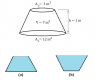
Problem Statement:
Both containers are just equal in volume and having same height; you can assume one is upside down of another. What is pressure at the bottom of the containers. Let's say left side is container 1 and one on right side is 2.
Relevant equation:
My attempt:
Thought 1: Pressure will be equal at bottom for both the cases; and force to the bottom we can find with multiplying the respective bottom surface areas.
Thought 2: As volume and density of both the liquid is same; so the mass. When we draw free body diagram of the liquid, it appears the forces will be equal at bottom will be equal not the pressure.