Forerunner546
- 3
- 0
Homework Statement
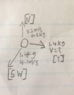
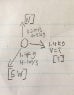
A pumpkin of mass 3.30kg at rest on a smooth frictionless plane, explodes into 3 pieces in the horizontal plane. A .50kg piece flies to the North at 3.2m/s. A 1.4kg piece flies off (SW) at 4.1m/s.
What is the speed, direction and mass of the third piece?
Homework Equations
M1V1o + M2V2o = M1V1f + M2V2f
The Attempt at a Solution
I assumed the piece was 1.4kg as I subtracted the original pumpkins mass by the known fragmentary masses. I used the conservation of momentum to subtract the original pumpkins mass and velocity by the unknown fragment and equaled it to the two known pieces. M1V1o - M3V3f = M1V1f + M2V2f
This yielded -5.2 as a velocity which seems wrong, and I have no idea how to find the direction of the third piece and no angles were included.