Joshuaniktas
- 1
- 0
Hi there, I have tried to do these questions but I don't understand. Any help would be appreciated!
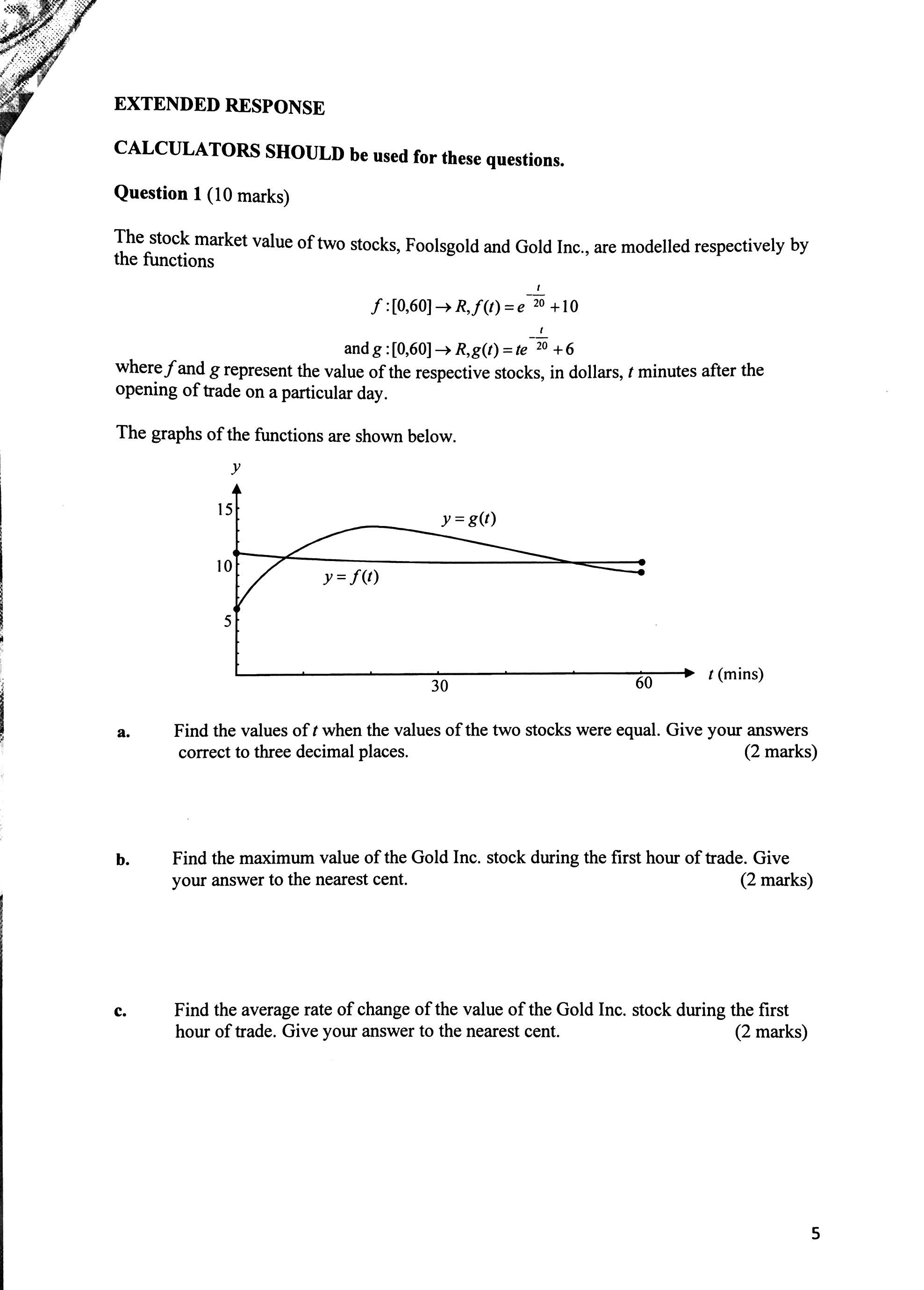
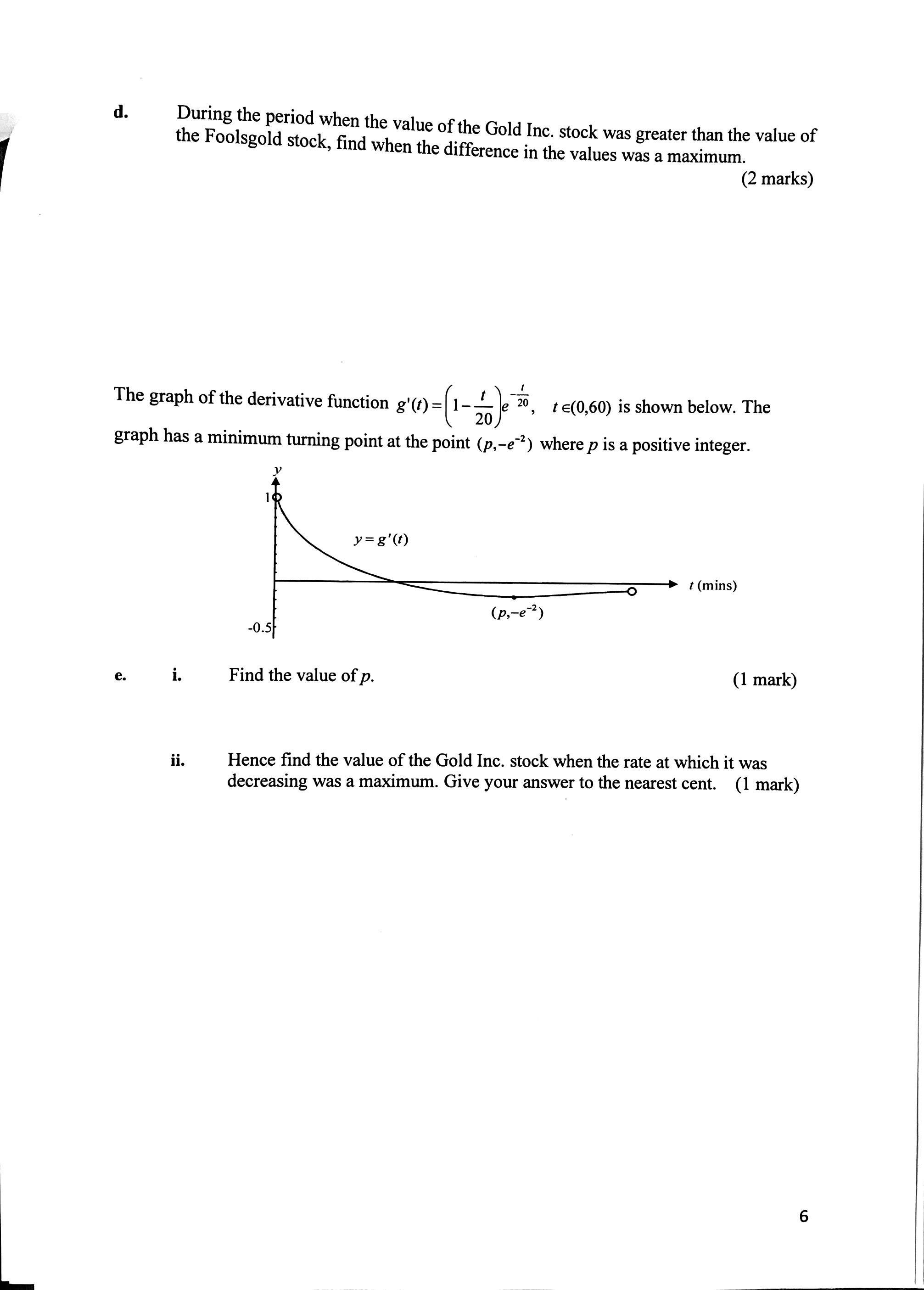
The discussion focuses on solving exponential functions using a computer algebra system (CAS). Specifically, the equation analyzed is $$e^{-\frac{t}{20}} + 10 = te^{-\frac{t}{20}} + 6$$, which simplifies to $$4 = te^{-\frac{t}{20}} - e^{-\frac{t}{20}}$$. The numeric approximations for the solutions are found to be approximately $$t \approx 6.54997$$ and $$t \approx 50.1865$$. Additionally, a graph of the function $$y = xe^{-\frac{x}{20}} + 6$$ is discussed for further analysis.
PREREQUISITESStudents and educators in mathematics, particularly those focused on calculus and algebra, as well as anyone interested in using CAS for solving complex equations.