artriant
- 35
- 2
When a mass is in a circular motion and suddenly gets released by its centripetal force, it will continue traveling in a straight path (tangent to the circle and perpendicular to the radius in the moment of release) if no other forces acting.
So let’s make a case: We have a space centrifuge r=250m that provides "an artificial gravity or an accelaration equal to moons gravity, the entire structure is cruising freely in free fall let's say in GEO orbit. The linear speed at the circumference (which is also happening to be the ground inside the space station), is Uc =20.13715 m/s. Our test subject is going to be an apple that is fixed inside the rotating frame and “hovering” 10 m above the “ground”, the point exactly below the apple we will nickname it “ground zero”, and we will also assume that we don’t have any air or obstacles or other external forces. Now when we let the apple to “fall” observers inside in the outer region of the space station - near it, will witness that it follows a curved path which is affected by the Coriolis Fictious Force. Problem is that i can't use physics, so i used geometry to predict the offset.
We draw the station (a big circle)in the blackboard and a straight line perpendicular to the position of the apple in the moment of release. We found the impact point but did we just solved the problem? Nop, the linear speed of the apple is different than the linear speed of the outer region mainly because we have 10m difference in radius. To find the U of the apple (Ua) we can use the linear speed at the circumference Uc and because it is proportional to r we can find for any raidus with the rule of three:
Ua (m/s) / 240(m) = Uc (m/s) / 250(m),,, so Ua (m/s)=240(m)*Uc (m/s)/250(m) => Ua=19,331664(m/s)
Right after the release, the apple will travel freely 70(m) in a straight line AB of a triangle ABC that has the C connected to the center of the station (center of rotation), with angles ∠ACB=16.26° ∠ CBA=73,74° ∟BAC=90°
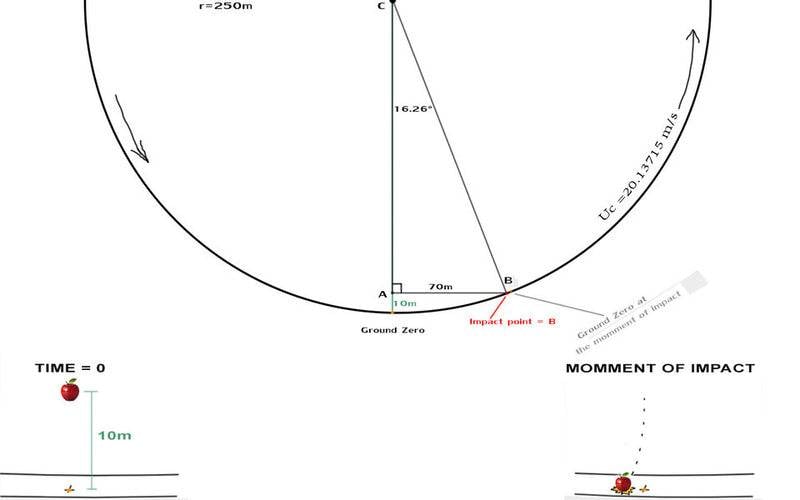
Since we know the speed of the apple we can find the amount of time (t1) till it travels from point A to point B, rule of three: t1(sec)/70m 1sec/20.13715m => t1sec=70*1/20.13715 = t1=3,621 (sec)
So regardless of path in our experiment we already know that the apple is going to “fall” for 3,621 (sec) till it colides with the ground.
In the same amount of time, the host is going to rotate 16.26°
That angle coresponds to a length of arc X1(m) = 3,621(sec)*20.13715(m)/1(sec) => X1= 72,9166~ (m)
The length of the arc (in the circumference) from ground zero to the hit point 'B' is :
X2/quarter of circle (meters)= 16,26/90 (degrees) =>X2=(392,7*16,26)/90 => X2=70,9478m
If we subtract X2-X1 we get the offset measured in a length of arc = 1.968866~ m (absolute value)
So a camera focused on the ground zero, will record an apple that is missing the “target” (ground zero)by a whole 1,96 m, the measuring tool should be placed touching the ground parallel to circumference and against the direction of spinning, the apple kind of left behind while falling, like it couldn’t catch up the faster moving ground of the space station. Others explain that behavior of the falling apple inside a space centrifuge "like it is blown by a wind that flows against the direction of spinning".
----
My question is how do i solve the same problem with physics, i can predict the ofset here which is handy, but can't predict the exact path, or where the apple is going to be at any point in time, in a rotating reference frame. I really want to visualize that for varius setups. I think this will be very baisic in the future. Thanks for any replies.
So let’s make a case: We have a space centrifuge r=250m that provides "an artificial gravity or an accelaration equal to moons gravity, the entire structure is cruising freely in free fall let's say in GEO orbit. The linear speed at the circumference (which is also happening to be the ground inside the space station), is Uc =20.13715 m/s. Our test subject is going to be an apple that is fixed inside the rotating frame and “hovering” 10 m above the “ground”, the point exactly below the apple we will nickname it “ground zero”, and we will also assume that we don’t have any air or obstacles or other external forces. Now when we let the apple to “fall” observers inside in the outer region of the space station - near it, will witness that it follows a curved path which is affected by the Coriolis Fictious Force. Problem is that i can't use physics, so i used geometry to predict the offset.
We draw the station (a big circle)in the blackboard and a straight line perpendicular to the position of the apple in the moment of release. We found the impact point but did we just solved the problem? Nop, the linear speed of the apple is different than the linear speed of the outer region mainly because we have 10m difference in radius. To find the U of the apple (Ua) we can use the linear speed at the circumference Uc and because it is proportional to r we can find for any raidus with the rule of three:
Ua (m/s) / 240(m) = Uc (m/s) / 250(m),,, so Ua (m/s)=240(m)*Uc (m/s)/250(m) => Ua=19,331664(m/s)
Right after the release, the apple will travel freely 70(m) in a straight line AB of a triangle ABC that has the C connected to the center of the station (center of rotation), with angles ∠ACB=16.26° ∠ CBA=73,74° ∟BAC=90°
Since we know the speed of the apple we can find the amount of time (t1) till it travels from point A to point B, rule of three: t1(sec)/70m 1sec/20.13715m => t1sec=70*1/20.13715 = t1=3,621 (sec)
So regardless of path in our experiment we already know that the apple is going to “fall” for 3,621 (sec) till it colides with the ground.
In the same amount of time, the host is going to rotate 16.26°
That angle coresponds to a length of arc X1(m) = 3,621(sec)*20.13715(m)/1(sec) => X1= 72,9166~ (m)
The length of the arc (in the circumference) from ground zero to the hit point 'B' is :
X2/quarter of circle (meters)= 16,26/90 (degrees) =>X2=(392,7*16,26)/90 => X2=70,9478m
If we subtract X2-X1 we get the offset measured in a length of arc = 1.968866~ m (absolute value)
So a camera focused on the ground zero, will record an apple that is missing the “target” (ground zero)by a whole 1,96 m, the measuring tool should be placed touching the ground parallel to circumference and against the direction of spinning, the apple kind of left behind while falling, like it couldn’t catch up the faster moving ground of the space station. Others explain that behavior of the falling apple inside a space centrifuge "like it is blown by a wind that flows against the direction of spinning".
----
My question is how do i solve the same problem with physics, i can predict the ofset here which is handy, but can't predict the exact path, or where the apple is going to be at any point in time, in a rotating reference frame. I really want to visualize that for varius setups. I think this will be very baisic in the future. Thanks for any replies.
