Nirmal Padwal
- 41
- 2
- Homework Statement
- Remembering that helicity is conserved at high energies,
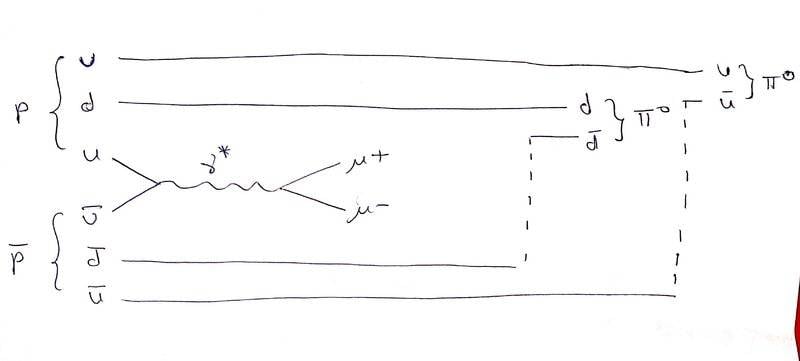
a) Draw a typical diagram for ##\mu^+ \mu^-##-pair production, with an invariant mass around 30 GeV, in unpolarised ##p\bar{p}## collisions.
b) Derive an expression for the angular distribution (with respect to the ##\bar{p}## direction) of ##\mu^+## in the ##\mu^+\mu^-##, centre-of-mass system.
(Hint: You will need to look up the appropriate ##d^j_{m'm}## rotation matrix elements)
- Relevant Equations
- 1) ##d^1_{11} = \frac{1}{2}(1+\cos\theta)##
2) ##d^1_{-11} = \frac{1}{2}(1-\cos\theta)##
I was able to solve b) but I am confused for a). I understand that in the proton-antiproton collision, only two quarks (one from proton and other from anti-proton) can be combined to get a virtual photon that in turn creates muon and anti-muon. I don't understand what would happen to the other quarks? Since single quarks cannot exist independently, I think maybe they combine to form mesons. Is that correct? But which meson? If I take ##u## and ##\bar{u}## from ##p## and ##\bar{p}## respectively (please check the feynman diagram below), I am still left with ##u,d,\bar{u},\bar{d}##. Do they combine to give two ##\pi^0##s or ##\pi^+\pi^-##?