Feynman path integral and events beyond the speed of light

[kurt101]

TL;DR Summary

Do events that can't actually happen because of the speed of light limitations contribute to probabilities that are calculated using the Feynman's path integral method?

In Richard Feynman's book "The Strange Theory of Light and Matter", in chapter 2, he explains how to calculate the probability that light from some source will be reflected by a mirror and be detected at some location. He explains how you sum up all of the probability amplitudes (represented as vectors) for each way light can reflect off of a mirror and end up at the detector and then square this result to get the final probability. Here is the illustration of this:

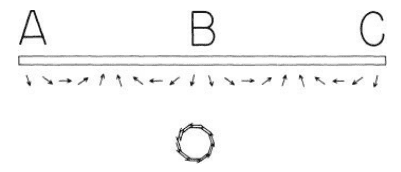
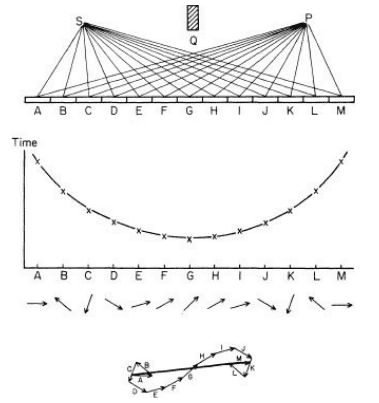Feynman then explains how the probability amplitudes of reflections around A and B tend to cancel out and thus don't contribute very much to the final probability. Here is the illustration of this:

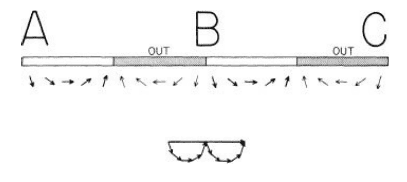
Feynman then explains that if you remove sections of the mirror at A and B that you can change the contributions of the probability amplitudes around A and B so that they do contribute significantly to the final probability. Here is the illustration of this:

My Question:
What happens if you turn on the light source for a small amount of time and only detect the light that could have reflected from the middle of the mirror (around say E through I) in the amount of time that it takes light from the source traveling at the speed of light to reflect and arrive at the detector. In this case would you eliminate the contributions to the final probability from the reflections around A and B because they could not have possibly contributed because of the speed of light?

 

[PeroK]

There's no certainty in when a photon is emitted, so you can't have QED on the one hand and classical precise events in spacetime on the other.

In fact, the arguments in that book generally rely on this uncertainty in order to have the interference in the first place.

Remember also that interference is generally a photon interfering with itself and not different photons interfering with each other. Although the full picture is more complicated than that.

 

[kurt101]

There's no certainty in when a photon is emitted, so you can't have QED on the one hand and classical precise events in spacetime on the other.

In fact, the arguments in that book generally rely on this uncertainty in order to have the interference in the first place.

But you can know that the amount of time the light source was turned on is well between the times it took for reflection in the middle of the mirror (say source -> G -> detector) and the time it took for reflection at the end of the mirror (say source -> A -> detector). So you can run the experiment with these constraints and see if having the missing sections of mirror at A and B has any change on the probability. And so does having or not having the sections with this constraint change the probability?

And maybe there would be some variation in light detection based on the uncertainty, but if you ran enough trials the uncertainty should wash out.

 

[hutchphd]

If you manipulate the light in time as you describe it will necessarilly not be monochromatic and you will wash out potential interference patterns. In rereading this I am uncertain as to what the actual question is.

 

[PeroK]

But you can know that the amount of time the light source was turned on ...

The emission of a photon, as with practically everything in quantum theory, is a probabilistic event. If you try to have a photon at spacetime coordinates $(t, x, y, z)$ moving with speed $c$ in some direction $\vec n$, then that is not quantum theory in the first place. That's a classical view of the photon as a massless particle with a classical trajectory.

QED by Feynman, if it does anything, is trying to get you NOT to think of light like that!

 

[PeterDonis]

Summary:: Do events that can't actually happen because of the speed of light limitations contribute to probabilities that are calculated using the Feynman's path integral method?

In the path integral method photons do not have a well-defined "speed"; paths in which photons travel at different speeds all contribute to the path integral. In more technical language, worldlines which are timelike and spacelike, as well as worldlines which are null, make nonzero contributions to the path integral.

In many cases (such as light traveling over long distances in free space), the contributions to the path integral from any worldlines other than the classical null worldline are negligible; in these cases, we can view the light as simply traveling at the speed of light through free space. But there are also many cases where this is not true. The general rule is that you must include in the path integral all paths that are not forbidden by some condition of the problem (such as the presence of an opaque screen), even if those paths would make no sense classically.

 

[vanhees71]

One should take the "null world lines" as what they really are, namely the characteristics of the eikonal equation, and this is just an approximate solution of the wave equation of the electromagnetic field. The phasor approach in Feynman's popular book is nothing else than the classical refraction theory in Fraunhofer approximation, i.e., it solves the wave equation for the electromagnetic field, and thus it is consistent with the propagation of these waves with the speed of light.

 

[PeterDonis]

One should take the "null world lines" as what they really are, namely the characteristics of the eikonal equation, and this is just an approximate solution of the wave equation of the electromagnetic field. The phasor approach in Feynman's popular book is nothing else than the classical refraction theory in Fraunhofer approximation, i.e., it solves the wave equation for the electromagnetic field, and thus it is consistent with the propagation of these waves with the speed of light.

For the specific examples Feynman discusses, which all involve light propagation (reflection off a mirror, diffraction gratings, bending when passing from one medium to another), yes, he is only considering null paths through spacetime (different paths through space, but which are all traversed at the speed of light and therefore have different travel times from source to receiver). But the path integral formulation is much more general; for example, when modeling a static force between charged objects, the path integral will have significant contributions from timelike and spacelike paths through spacetime.

 

[kurt101]

If you manipulate the light in time as you describe it will necessarilly not be monochromatic and you will wash out potential interference patterns.

Why does turning on and off a monochromatic light source make the light from that source NOT monochromatic?

In rereading this I am uncertain as to what the actual question is.

I will try phrasing it again.

To make my question as clear as possible I am using the same context as Feynman used in chapter 2 of his book "The Strange Theory of Light and Matter" where he describes how to calculate the probability of light from a monochromatic source reflecting off a mirror to a detector. After he explains the basic procedure he goes on to explain how removing sections at the end of the mirror can alter the probability that light reaches the detector. Ok with this part?

My question involves taking the Feynman scenario and putting the following constraints on the light source and the detector. For clarity sake I will call this my experiment and to make the sequence of events clear, I will put in some time values.

Lets say the following:
It takes roughly 5 seconds for light to travel from the light source to the middle of the mirror (point G in the diagram) to the detector.
It takes roughly15 second for light to travel from the light source to the end of the mirror (point A in the diagram) to the detector.

In my experiment:
At 0 seconds, I turn on the light source and start recording at the detector.
At 10 seconds, I turn off the light source and stop recording at the detector.

In the first version of my experiment, I make no changes to the mirror. The mirror at point A and B look like:

In the second version of my experiment, I remove sections at the end of the mirror. The mirror at point A and B now looks like:

I run many trials of both versions of my experiment. Over all my trials I compare the average amount of light I measured in the first version of my experiment to the average amount of light measured in the second version of my experiment. Is the amount of light measured between the first version of my experiment the the same or different than the second version of my experiment?

 

[PeroK]

Lets say the following:
It takes roughly 5 seconds for light to travel from the light source to the middle of the mirror (point G in the diagram) to the detector.
It takes roughly15 second for light to travel from the light source to the end of the mirror (point A in the diagram) to the detector.

Light can travel from Earth four times further than the Moon in 5 seconds.

 

[PeterDonis]

Why does turning on and off a monochromatic light source make the light from that source NOT monochromatic?

Because one of the requirements for a source to be truly monochromatic is that it emits light continuously forever, infinitely into the past and infinitely into the future. Which means, of course, that no real light source is ever truly monochromatic.

 

[kurt101]

The emission of a photon, as with practically everything in quantum theory, is a probabilistic event. If you try to have a photon at spacetime coordinates $(t, x, y, z)$ moving with speed $c$ in some direction $\vec n$, then that is not quantum theory in the first place. That's a classical view of the photon as a massless particle with a classical trajectory.

QED by Feynman, if it does anything, is trying to get you NOT to think of light like that!

I am trying to understand how QED applies to the real world. I think that was one of the major reasons Feynman wrote the book. I think that is the major purpose of quantum mechanics. In the real world, when I turn on the light, I expect to detect photons in the detector at some later time that is roughly the distance of the shortest path of light divided by 3 x 10^8 m/s. I don't know how the light actually traveled from the source to the detector and I have tried to avoid any kind of interpretation in the presentation of my question.

Light can travel from Earth four times further than the Moon in 5 seconds.

Ha, ha, I guess the mirror is very large.

 

[kurt101]

In the path integral method photons do not have a well-defined "speed"; paths in which photons travel at different speeds all contribute to the path integral. In more technical language, worldlines which are timelike and spacelike, as well as worldlines which are null, make nonzero contributions to the path integral.

In many cases (such as light traveling over long distances in free space), the contributions to the path integral from any worldlines other than the classical null worldline are negligible; in these cases, we can view the light as simply traveling at the speed of light through free space. But there are also many cases where this is not true. The general rule is that you must include in the path integral all paths that are not forbidden by some condition of the problem (such as the presence of an opaque screen), even if those paths would make no sense classically.

I have done a lot of searching for answers related to my question prior to posting it. I get the sense that there is a lot of uncertainty on what actually contributes to the probability in the path integral formulation. While I believe what you told me is correct, you left it sufficiently vague (i.e. "The general rule is that you must include in the path integral all paths that are not forbidden by some condition of the problem") and so I not able to answer my question with this rule. In other words I don't know what those conditions are.

 

[PeterDonis]

I get the sense that there is a lot of uncertainty on what actually contributes to the probability in the path integral formulation.

No, there is no uncertainty at all. The math is perfectly clear.

For you, the problem is that you aren't looking at the math. You're looking at various people's attempts to describe what the math is saying in ordinary language. And there is no way to do that with 100% accuracy because our ordinary language simply doesn't have the words or the concepts required. That's why physicists don't use ordinary language to do physics; they use math.

I don't know what those conditions are.

There will be some paths through spacetime that are forbidden because of the presence of something (such as an opaque screen, which was the example I gave) that absorbs light. (You could, if you really wanted to, include the details of the absorption of the light by that something in your analysis, but all that would do is complicate the math even more to get the same answer--that none of that light makes it to your detector.)

 

[vanhees71]

For the specific examples Feynman discusses, which all involve light propagation (reflection off a mirror, diffraction gratings, bending when passing from one medium to another), yes, he is only considering null paths through spacetime (different paths through space, but which are all traversed at the speed of light and therefore have different travel times from source to receiver). But the path integral formulation is much more general; for example, when modeling a static force between charged objects, the path integral will have significant contributions from timelike and spacelike paths through spacetime.

But of course the path integral for relativistic QT is not a path integral over paths in phase space of point particles (or after integrating out the momenta, if they appear only quadratically in the action, over paths in configuration space) in non-relativistic QT ("1st quantization") but a path integral over field configurations.

 

[kurt101]

No, there is no uncertainty at all. The math is perfectly clear.

If it is so clear to you then help me understand how to apply the algorithm Feynman describes to answer the question I am asking.

 

[kurt101]

@vanhees71 I have read many of your discussions around microcausality in the context of QFT. For example you wrote:

This together with the fact that a local relativistic QFT cannot describe any faster-than-light signal propagation (due to the microcausality built in this kind of relativistic QFTs) one must conclude that the correlation is not caused by the local measurements on each photon at far distant places but it is due to the preparation in the entangled state.

Does the microcausality condition require local (in a spatial sense) preparation?

In the scenario I am discussing in this thread where removing sections of a mirror (i.e. the grating) affect the probability of the light being detected; what is the (local?) preparation between the light source and the grating?

Ultimately in this thread, I am trying to understand how something distant affects where the light ends up. I am trying to understand this in the context of the QED algorithm Feynman describes.

For someone who truly understands QFT, my question about whether having the grating or not has an effect on the detection probability with the time window constraint I have added, should be trivial to answer.

 

[Nugatory]

If it is so clear to you then help me understand how to apply the algorithm Feynman describes to answer the question I am asking.

The problem here is that we can’t do anything with a description of an algorithm. To do something we need the real thing, and “QED: The strange theory….” is not that; it’s an extended multi-page analogy that offers non-specialists some intuition for how local interference can yield many of the macroscopic behaviors of light. You should not be surprised to find that its math-free toy model becomes vague and mushy when you push it.

One particularly important limitation of the model is that it does not work for light that is switched on and off (more precisely, is not kept on for a time that is long compared with the time it takes for light to reach all parts of the setup). Thus it‘s not a good place to start when you’re trying to understand which paths to include and why some seem to be arbitrarily excluded. The real theory, expressed mathematically, does not have this limitation.

 

[gentzen]

If it is so clear to you then help me understand how to apply the algorithm Feynman describes to answer the question I am asking.

hutchphd anwered your intial question: "If you manipulate the light in time as you describe it will necessarilly not be monochromatic and you will wash out potential interference patterns." You slightly modified your question in response to his answer, but basically his answer still applies. If you don't understand his answer in the context of your initial question, then you will understand it even less in the context of your modified question.

In QED, Feynman describes how coherent superposition works. But what happens in your setup is partial coherent superposition, i.e. an incoherent average over coherent superpositions (what hutchphd described as "... will wash out ..."). Perhaps trying to understand the picture and explanations on the last slide of this extract will help you a bit.

To make everything even more confusing, partial coherence can be "reduced" to full coherence by going to a (church of the) larger Hilbert space. But if you don't already understand partial coherence, this construction won't help you either.

 

[PeterDonis]

If it is so clear to you then help me understand how to apply the algorithm Feynman describes to answer the question I am asking.

You can't apply the specific algorithm Feynman describes to the specific case given in your OP, because, as has already been pointed out, his algorithm doesn't work for light sources that are switched on and off. More precisely, it doesn't work for light sources that are switched on and off on a time scale comparable to the time scale of the experiment you are doing.

You can use the math of QED directly to answer a question like the one you ask in your OP, but, as has already been pointed out, the math of QED is not the same as the heuristic ordinary language description that Feynman gives. If you really want to learn how to apply QED to general cases, not just the specific cases Feynman describes in his book, you will need to learn how to use the math of QED. There are no shortcuts that let you use vague ordinary language to actually do physics.

 

[PeterDonis]

You can use the math of QED directly to answer a question like the one you ask in your OP, but, as has already been pointed out, the math of QED is not the same as the heuristic ordinary language description that Feynman gives.

Note that the last paragraph of my post #14 was an attempt to at least convey a more general sense of what the math of QED is doing, beyond what Feynman says in his book. There are other possible reasons besides the presence of an opaque screen for particular paths through spacetime being forbidden: one such reason is that the light source is turned off, so paths through spacetime that originate from the source when it is turned off will not have any nonzero amplitude associated with them. But you can't analyze such cases using the heuristic ordinary language picture Feynman gives in his book.

 

[DrChinese]

Is the amount of light measured between the first version of my experiment the the same or different than the second version of my experiment?

1. You already know that if a diffraction grating is placed at appropriate spots on the mirror, there will be no contribution to the final result from that section. Any way that contribution is alternatively excluded gives the same results as if a diffraction grating were present. There is no faster-than-light effect present in any version of this scenario.2. As a practical matter, using some classical reasoning to consider your version of the experiment: In a femtosecond (10^-15 seconds), light travels about about 333 nanometers (nm) - little shorter than a wavelength of visible light. The difference X in distance light travels when it is reflected from the middle (your B) versus when it is further away by a single wavelength (i.e. ever so slightly closer to your A or C) is extremely small. Using some "reasonable" parameters for visible light, approximately 45 degree angle of incidence, 1000 wavelength distance to mirror, back of a napkin calculations... that X works out to be on the order of magnitude of 1 nanometer (nm). That translates to a time window of roughly 0.003 femtoseconds.

In other words, we would need to nail down the precise time of emission AND detection to less than approximately .003 femtoseconds to be able to perform this experiment. The best detectors today have a comparable resolution of no better than 1 picosecond (1000 femtoseconds), or nearly a million times longer that what you'd need to even think about running your experiment. And that doesn't begin to consider a variety of quantum effects and uncertainty you'd encounter.3. Think of the Feynman paths as follows: Because of inherent uncertainty in photon emission times: a detection at experimentally precise (if there was such a thing) time T3 could result from a slightly shorter path traversed by a photon B emitted at time T2, or a slightly longer path traversed by a photon A emitted slightly earlier at time T1. Both of those possibilities contribute to the result. You could perform this experiment a photon at a time, but it is not possible to force (or restrict) a single photon to be emitted at a specific time with sufficient resolution to distinguish between scenarios A and B. To the extent that you could perform this impossible task, you would only succeed in demonstrating what we already know would occur. And that would not show any FTL effect at all.

 

[CelHolo]

It's best not to try to imagine the Feynman paths as real processes or worry about FTL paths and so on. Most of the "paths" contributing to the path integral aren't even functions but distributions and so in no sense describe actual paths, i.e. assign a position for each time.

 

[kurt101]

hutchphd anwered your intial question: "If you manipulate the light in time as you describe it will necessarilly not be monochromatic and you will wash out potential interference patterns." You slightly modified your question in response to his answer, but basically his answer still applies. If you don't understand his answer in the context of your initial question, then you will understand it even less in the context of your modified question.

I added more detail to my question, but did not change it. In Feynman's book, chapter 2 that I used as the basis for my description, the light source is described as monochromatic and I left that detail out. Here is the actual quote from the book:

"At S we have a source that emits light of one color at very low intensity (let’s use red light again). The source emits one photon at a time." - Feynman, Richard P.. QED: The Strange Theory of Light and Matter (Princeton Science Library) (p. 38). Princeton University Press. Kindle Edition.

Also I do not say in my question that the light source emits one photon at a time, but I do not think that is relevant to my question. Is it important to the result at the detector that the light source emits 1 photon at a time?

In QED, Feynman describes how coherent superposition works. But what happens in your setup is partial coherent superposition, i.e. an incoherent average over coherent superpositions (what hutchphd described as "... will wash out ..."). Perhaps trying to understand the picture and explanations on the last slide of this extract will help you a bit.

I understand the light source in Feynman's example is not coherent; at least in the sense that he does not describe it as a laser where light is in phase. That said, I don't understand how turning on the light makes the light any different (i.e. more or less coherent) than how Feynman already describes it. Unless I am mistaken about Feynman's example and he does mean to imply that is light source is fully coherent even though he never states it. I would be surprised if this is the case.

 

[PeroK]

I added more detail to my question, but did not change it. In Feynman's book, chapter 2 that I used as the basis for my description, the light source is described as monochromatic and I left that detail out. Here is the actual quote from the book:

"At S we have a source that emits light of one color at very low intensity (let’s use red light again). The source emits one photon at a time." - Feynman, Richard P.. QED: The Strange Theory of Light and Matter (Princeton Science Library) (p. 38). Princeton University Press. Kindle Edition.

Also I do not say in my question that the light source emits one photon at a time, but I do not think that is relevant to my question. Is it important to the result at the detector that the light source emits 1 photon at a time?
I understand the light source in Feynman's example is not coherent; at least in the sense that he does not describe it as a laser where light is in phase. That said, I don't understand how turning on the light makes the light any different (i.e. more or less coherent) than how Feynman already describes it. Unless I am mistaken about Feynman's example and he does mean to imply that is light source is fully coherent even though he never states it. I would be surprised if this was the case.

So, why don't we just stick with one photon? The whole point of that section is to describe how the probability of the photon being detected depends on the diffraction grating.

Why have you brought all these added compexities into the equation?

 

[kurt101]

There are other possible reasons besides the presence of an opaque screen for particular paths through spacetime being forbidden: one such reason is that the light source is turned off, so paths through spacetime that originate from the source when it is turned off will not have any nonzero amplitude associated with them.

This sounds promising to helping me answer my question, but in the context of everything else told to me, I am far from certain.

What about when the the light source is turned on? Do paths that don't yet exist through spacetime (outside of the light source's light cone), have a nonzero amplitude?

 

[PeroK]

What about when the the light source is turned on? Do paths that don't yet exist through spacetime (outside of the light source's light cone), have a nonzero amplitude?

You may have completely lost the point of this treatment of QED. I think you should ask yourself whether you are intent on studying the material in Feynman's book, or whether you'd rather let your mind wander onto vague and superfluous questions.

Perhaps I'm too harsh. If so I apologise. But, if you were my student I'd tell you to knuckle down and concentrate.

 

[gentzen]

I understand the light source in Feynman's example is not coherent; at least in the sense that he does not describe it as a laser where light is in phase.

He describes the light source as monochromatic. This is what makes it coherent. To get quasi-monochromatic light from a non-laser source, you have to filter out most frequencies, and only keep a small portion of the frequency spectrum. That is typically still wider than for light from a laser, but the coherence length can be made longer than the distance-differences in your optical instruments. And that is enough for treating the light as quasi-monochromatic.

That said, I don't understand how turning on the light makes the light any different (i.e. more or less coherent) than how Feynman already describes it.

Let me first descibe it in Feynman's photon picture. Assume that each photon would have exactly one frequency, and nicely form a coherent superposition with itself. If different photons have slightly different frequencies, then their interference patterns are slightly different. And the sum of those interference patterns no longer shows sharp interference peaks, but appears washed out. But to see an interference pattern at all, you must look at the image produced by many photons, so all you can see is the washed out pattern.

If your light has the frequency f, and you switch it on for t seconds, then you end up with an frequency distribution in the range f +- 1/t. If f is big compared to 1/t, then it makes sense to talk of quasi-monochromatic light. And if c*t is big compared to the distance-differences in your optical instruments, then treating the light as monochromatic should work well.

 

[kurt101]

1. You already know that if a diffraction grating is placed at appropriate spots on the mirror, there will be no contribution to the final result from that section.

It is actually the opposite in the example, the diffraction grating placed at the end of the mirror adds a contribution, but I could see where one placed at the middle of the mirror counteracts the contribution, and so I get what you are saying.

Any way that contribution is alternatively excluded gives the same results as if a diffraction grating were present.

I am not sure if I follow what you are saying. Are you saying that given the constraints of my experiment, you will see the same results with or without the diffraction grating? (i.e. were you giving a direct answer to my question?).

There is no faster-than-light effect present in any version of this scenario.

Ultimately this is what I want to understand. I have had trouble finding clear statements in any of the descriptions of the Fenman path integral (both with math and without) that clearly say contributions prohibited by the speed of light don't count.

That said, I still don't understand if contributions that are prohibited by the speed of light in my example are from the light sources perspective or say the mirror's perspective. Hopefully you understand what I am saying here and this would be a part 2 question for this thread and so I am reluctant to get into it too much before I am comfortable that I understand my current question.

2. As a practical matter, using some classical reasoning to consider your version of the experiment: In a femtosecond (10^-15 seconds), light travels about about 333 nanometers (nm) - little shorter than a wavelength of visible light. The difference X in distance light travels when it is reflected from the middle (your B) versus when it is further away by a single wavelength (i.e. ever so slightly closer to your A or C) is extremely small. Using some "reasonable" parameters for visible light, approximately 45 degree angle of incidence, 1000 wavelength distance to mirror, back of a napkin calculations... that X works out to be on the order of magnitude of 1 nanometer (nm). That translates to a time window of roughly 0.003 femtoseconds.

In other words, we would need to nail down the precise time of emission AND detection to less than approximately .003 femtoseconds to be able to perform this experiment. The best detectors today have a comparable resolution of no better than 1 picosecond (1000 femtoseconds), or nearly a million times longer that what you'd need to even think about running your experiment. And that doesn't begin to consider a variety of quantum effects and uncertainty you'd encounter.

I know my example is not a practical one, at least the numbers I gave, but it is the principle of the example that is important and I still have the understanding that in principle you can run my experiment. If that is not the case, and I am still missing something, please make that clear to me.

3. Think of the Feynman paths as follows: Because of inherent uncertainty in photon emission times: a detection at experimentally precise (if there was such a thing) time T3 could result from a slightly shorter path traversed by a photon B emitted at time T2, or a slightly longer path traversed by a photon A emitted slightly earlier at time T1. Both of those possibilities contribute to the result. You could perform this experiment a photon at a time, but it is not possible to force (or restrict) a single photon to be emitted at a specific time with sufficient resolution to distinguish between scenarios A and B. To the extent that you could perform this impossible task, you would only succeed in demonstrating what we already know would occur. And that would not show any FTL effect at all.

If you changed the time constraint by adding additional detection time to be sure scenarios A and B (with and without the grating) should give a different result; then ran scenarios A and B many times; then took the averages; I would expect on average you would see a consistent difference between A and B, where scenario B with the grating that add contributions would on average detect more photons than A.

 

[kurt101]

You may have completely lost the point of this treatment of QED. I think you should ask yourself whether you are intent on studying the material in Feynman's book, or whether you'd rather let your mind wander onto vague and superfluous questions.

Perhaps I'm too harsh. If so I apologise. But, if you were my student I'd tell you to knuckle down and concentrate.

That is an interesting perspective. I don't think my questions are vague or superfluous. I think understanding the constraints for any algorithm, formula, etc. is extremely important. So I don't know where you are coming from.

My goal is one of understanding out of curiosity and not one of learning QM so I can earn a living from it (at least not right now (no jokes here)) and so maybe that plays a part in the types of questions I ask. I am biased towards a causal deterministic perspective and tend to think the universe is not fundamentally statistical and so maybe that bias shows (certainly obvious in my earlier threads) and plays a part in the types of questions I ask. That said, I enjoy reading the different perspectives on this forum and I am open to all well supported positions.

You also said "knuckle down and concentrate". I do read carefully most everyone's responses and try very hard to understand what is being said to me. So I hope you are not saying this because you don't think I am not reading or not trying to understand what is being said to me. If I ask more questions or try to clarify where I am coming from that does not mean I am rejecting what others are telling me. It might mean I still don't understand and/or I think I have been misunderstood.

 

[kurt101]

So, why don't we just stick with one photon? The whole point of that section is to describe how the probability of the photon being detected depends on the diffraction grating.

I am ok with 1 photon at a time versus many. I did not specify either way. I still don't think it matters for my question.

Why have you brought all these added compexities into the equation?

Because I am trying to understand how distant objects (e.g. the grating) affect the result. Its kind of like what others are telling me, the ordinary language does not matter, you have to understand the math. However in my case I would say it is the experiment that ultimately tells me the truth and while I don't doubt the math is correct from some perspective, math obviously has its limitations on where and how it can be used, and so it is helpful for me to understand what the actual experiment says.

 

[PeterDonis]

I do not say in my question that the light source emits one photon at a time, but I do not think that is relevant to my question. Is it important to the result at the detector that the light source emits 1 photon at a time?

It is important to the result at the detector to know what state the light emitted from the source is in. Saying "the source emits one photon at a time" does not tell you that. That is one of the key limitations of trying to learn physics from a pop science book written in ordinary language--even one by Feynman, who was one of the best physicists I know of at minimizing the distortion inherent in any such presentation.

The issue here, which is not necessarily important to the exposition Feynman was trying to make, but is very important if you are actually trying to understand the underlying physics in detail, is that "monochromatic" light is not in an eigenstate of photon number. "Monochromatic" light (I put the term in quotes because of the issue already raised, that truly "monochromatic" light can only be emitted by a source that emits light forever), such as light emitted by a laser, so called because (at least to whatever level of approximation is appropriate for the specific problem) it has a well-defined frequency, is in a coherent state. A coherent state does not have a well-defined photon number, since it is not in an eigenstate of photon number. So it is really not correct to describe such a source as emitting "one photon at a time". A strictly correct statement would be something like "the intensity of the source is such that the expected number of clicks at the photon detector over some standard interval of time is one". (Note that it is the detector that produces discrete clicks, or some other discrete phenomenon, that we associate with the term "photon".)

An eigenstate of photon number is called a Fock state, and is a very different state that requires a very different type of source (one which is much more difficult to make than a laser; experiments have been done using such sources, but they are much less common). That is not the kind of source Feynman was talking about; he was talking about something like a laser.

 

[PeterDonis]

why don't we just stick with one photon?

Because, as I noted in my previous post just now, "one photon" is a misleading description of the actual state of the light emitted by the kind of source (something like a laser) that Feynman was talking about.

 

[PeterDonis]

What about when the the light source is turned on? Do paths that don't yet exist through spacetime (outside of the light source's light cone), have a nonzero amplitude?

You are not thinking correctly about spacetime. Spacetime includes time. A spacetime model already includes all the information about when (i.e., at what events in spacetime) the light source is turned on. Only paths originating from those events in spacetime will have a nonzero amplitude. There is no such thing as "paths that don't yet exist through spacetime"; spacetime is not something that "changes" as things happen. A spacetime model already includes all the information about everything that happens.

 

[PeterDonis]

Unless I am mistaken about Feynman's example and he does mean to imply that is light source is fully coherent even though he never states it.

If the light is monochromatic, it is in a coherent state, as I have already said. A source like an ordinary light bulb does not produce monochromatic light. You need something like a laser.